题目描述

新一届智能车大赛在 JL 大学开始啦！比赛赛道可以看作是由 $n$ 个矩形区域拼接而成（如下图所示），每个矩形的边都平行于坐标轴，第 $i$ 个矩形区域的左下角和右上角坐标分别为 $(x_{i,1} ,y_{i,1})$ 和 $(x_{i,2} ,y_{i,2} )$。

题目保证：$x_{i,1} <x_{i,2} =x_{i+1,1}$，且 $y_{i,1} < y_{i,2}$，相邻两个矩形一定有重叠在一起的边（如图中虚线所示），智能车可以通过这部分穿梭于矩形区域之间。

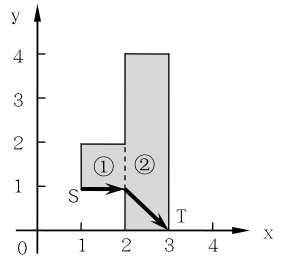
选手们需要在最快的时间内让自己设计的智能车从一个给定的起点 $S$ 点到达一个给定的终点 $T$ 点，且智能车不能跑出赛道。假定智能车的速度恒为 $v$ 且转向不消耗任何时间，你能算出最快需要多少时间完成比赛么？

输入格式

输入的第一行包含一个正整数 $n$，表示组成赛道的矩形个数。

接下来 $n$ 行描述这些矩形，其中第 $i$ 行包含 $4$ 个整数 $x_{i,1}, y_{i,1} , x_{i,2} , y_{i,2}$，表示第 $i$ 个矩形左下角和右上角坐标分别为 $(x_{i,1} , y_{i,1} )$ 和 $(x_{i,2} , y_{i,2} )$。

接下来一行包含两个整数 $x_S$，$y_S$，表示起点坐标。

接下来一行包含两个整数 $x_T$，$y_T$，表示终点坐标。

接下来一行包含一个实数 $v$（$1 \le v \le 10$），表示智能车的速度。

输出格式

仅输出一个实数，至少精确到小数点后第六位，为智能车完成比赛的最快时间。

对于每个测试点，如果你的输出结果和参考结果相差不超过 $10^{–6}$，该测试点得满分，否则不得分。

2
1 1 2 2
2 0 3 4
1 1
3 0
1.0

2.41421356

数据范围与提示

对于 $10\%$ 的数据，有 $n \le 1$.

对于 $30\%$ 的数据，有 $n \le 5$.

对于 $60\%$ 的数据，有 $n \le 200$.

对于 $100\%$ 的数据，有 $n \le 2000$.

保证所有坐标均为整数且绝对值不超过 $40000$.