atcoder#S8PC4F. Find the Route!
Find the Route!
题目描述
配点: 点
のグリッドがあります。左上の座標はで、右下の座標はです。
個のマスからは矢印が引かれており、座標から出ている矢印の先は、方向に、距離飛んだ場所、となっています。
また、同じマスから複数の矢印が出ていることはありません。
そこで、E869120は座標からへ矢印のみをたどって行きたいと思っています。
しかし、今の盤面だとゴールまで行けない場合があります。
そこで、E869120はグリッドを変えることにしました。しかし、グリッドを変えるのにはコストがかかります。
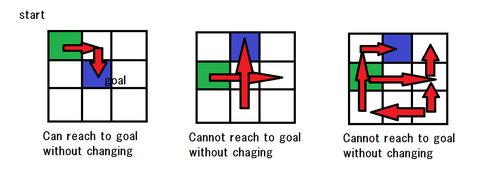
彼は、各矢印の方向や向きを以下のように変えることができる。
- 方向を変えるのにコストかかる。
- ・距離 の値を に変えるのに かかる。ただし、 は の絶対値。( は負の値も取りうる。また、はどの矢印についても共通の値である)
- ただし、の値を負にしてもよい。その場合、その矢印は逆向きになり、矢印の大きさは となる。
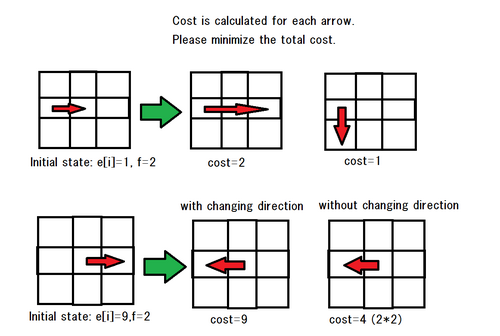
そのとき、スタートからゴールまで矢印のみをたどって行けるような盤面にするための、最小コストを求めてください。
ただし、矢印は一方通行であり、矢印の途中で曲がったりすることはできないとします。
ただし、グリッドを変えてもゴールにたどり着けない場合、「-1」と出力すること。
注意:ここでいう座標系は、(p1,p2)という形で表され、が小さい方が北側、 が小さい方が左側(西側)である。
输入格式
入力は以下の形式で標準入力から与えられる。
: : :
输出格式
スタートからゴールにたどり着くための、矢印を変えるコストの合計を最小値を1行に出力しなさい。
また、最後には改行を入れること。
4 4 2 2
1 1 2 2
1 1 E 1 1
1 2 E 2 2
4
1 4 2 10
1 1 1 4
1 1 E 1 4
1 3 W 1 4
14
1 8 4 9
1 3 1 6
1 1 E 7 2
1 8 W 7 5
1 3 W 2 5
1 6 E 2 8
14
14
提示
制約
- は
N,E,S,Wのどれかである。Nは上方向、Eは東方向。
小課題
小課題1 [ 点 ]
- H=1を満たす。
- W≦600を満たす。
小課題2 [ 点 ]
- H,W≦80を満たす。
小課題3 [ 点 ]
- H,W≦600を満たす。
小課題4 [ 点 ]
- 追加の制約はない。
