atcoder#S8PC3E. 円と三角形
円と三角形
题目描述
半径が の円があり、頂点 ~ が時計回りに並んでいます。
頂点は, 円周を 等分しています。
square1001は, つの頂点を選んで三角形を作ろうとしています。
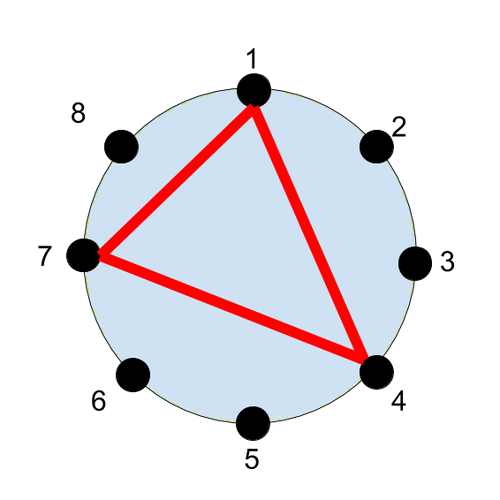
通りの作り方のうち, 面積が小さい順に数えて 番目となる三角形の面積を出力してください。
ただし, 面積が同じ場合は、面積だけを出力すればいいので順番は適当で構いません。
例えば, のとき, 次のようになります。
- 3頂点の番号が のとき, 面積
- 3頂点の番号が のとき, 面積
- 3頂点の番号が のとき, 面積
- 3頂点の番号が のとき, 面積
よって, 3番目の三角形の面積 となります。
問題作成者:E869120
输入格式
入力は以下の形式で標準入力から与えられる。
- 1行目に, 円周上にある点の数 と, 何番目の三角形かを表す整数 が, 空白区切りで与えられる。
输出格式
- 面積が小さい順から数えて 番目となる三角形の面積を出力しなさい。
- ただし, 絶対誤差または相対誤差が 以下であれば正解とみなされる。
题目大意
一个单位圆周上均匀地分布着n个点。 通过连接它们我们可以得到一堆(准确地说,是 个)三角形。 所以就需要您来求其中第k小的那一个的面积。 误差只要在 以内都是可以接受的。
Translated by @6ziv
4 3
1.000000000000000000
6 9
0.86602540378
12 220
1.29903810568
提示
制約
小課題
小課題1 [ 点 ]
小課題2 [ 点 ]
小課題3 [ 点 ]
- 追加の制約はない。
Sample Explanation 1
この入力例は問題文で説明したとおりです。
Sample Explanation 2
のとき, 面積が となるような頂点の選び方は 通り, 面積が となるような頂点の選び方は 通り, 面積が となるような頂点の選び方は 通りあります。 よって, 番目の三角形の面積は となります。
Sample Explanation 3
のとき, 三角形の作り方は 通りあります。 この中で面積が一番大きいのは正三角形となるときなので, 番目の三角形の面積は となります。
