atcoder#MUJINPC2017B. Row to Column
Row to Column
题目描述
縦 行、横 列の正方形状のマス目があります。 上から 行目、左から 列目のマスを と表します。
最初、各マスは白か黒です。 最初のマス目の配色は、正方形状に並ぶ文字 () として与えられます。 マス が白ならば は . であり、黒ならば は # です。
あなたは、マス目の配色を塗り替えるロボットを開発しています。 このロボットは次の操作を繰り返し行うことができます。
- 整数 , () をそれぞれ自由に選ぶ。 マス , , , の色をそれぞれ , , , として記憶する。 その後、マス , , , の色をそれぞれ , , , で塗り替える。
あなたの目標は、すべてのマスを黒にすることです。 すべてのマスを黒にすることが可能か判定し、可能ならば必要な操作回数の最小値を求めてください。
输入格式
入力は以下の形式で標準入力から与えられる。
输出格式
すべてのマスを黒にすることが可能ならば、必要な操作回数の最小値を出力せよ。 不可能ならば、代わりに -1 を出力せよ。
2
#.
.#
3
2
..
..
-1
2
##
##
0
3
.#.
###
.#.
2
3
...
.#.
...
5
提示
制約
- は
.または#である。
部分点
- 点分のテストケースでは、 が成り立つ。
Sample Explanation 1
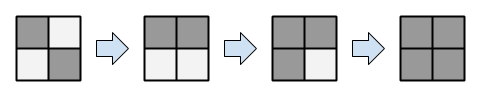
例えば、次のように操作を行うと、次図のようにマス目の配色が変わります。 - , と選んで操作を行う。 - , と選んで操作を行う。 - , と選んで操作を行う。