atcoder#CODEFESTIVAL2017QUALAE. Modern Painting
Modern Painting
Score : points
Problem Statement
Ringo got interested in modern art. He decided to draw a big picture on the board with rows and columns of squares constructed in the venue of CODE FESTIVAL 2017, using some people.
The square at the -th row and -th column in the board is represented by the pair of integers . That is, the top-left square is , and the bottom-right square is . Initially, the squares satisfying and are painted white, and the other (outermost) squares are painted black.
Ringo arranged people at some of the outermost squares, facing inward. More specifically, the arrangement of people is represented by four strings , , and , as follows:
- For each row except the top and bottom, if the -th character in is
1, place a person facing right at the square ; otherwise, do nothing. - For each row except the top and bottom, if the -th character in is
1, place a person facing left at the square ; otherwise, do nothing. - For each column except the leftmost and rightmost, if the -th character in is
1, place a person facing down at the square ; otherwise, do nothing. - For each column except the leftmost and rightmost, if the -th character in is
1, place a person facing up at the square ; otherwise, do nothing.
Each person has a sufficient amount of non-white paint. No two people have paint of the same color.
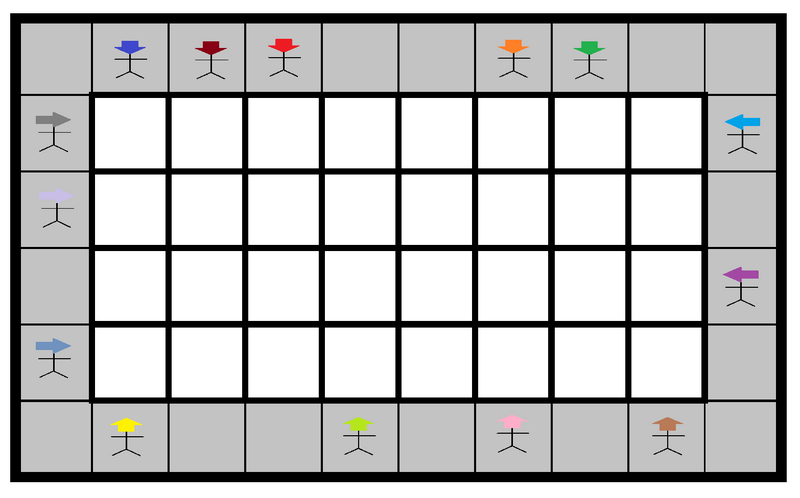
An example of an arrangement of people (For convenience, black squares are displayed in gray)
Ringo repeats the following sequence of operations until all people are dismissed from the venue.
- Select a person who is still in the venue.
- The selected person repeats the following action while the square in front of him/her is white: move one square forward, and paint the square he/she enters with his/her paint. When the square in front of him/her is not white, he/she stops doing the action.
- The person is now dismissed from the venue.
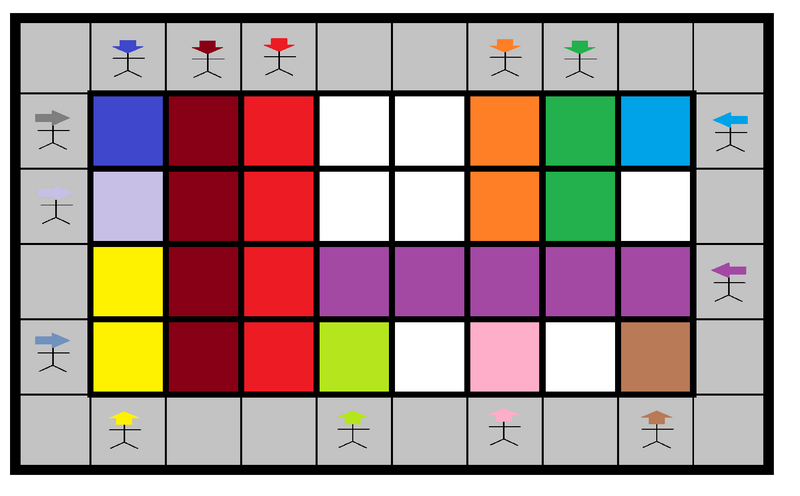
An example of a way the board is painted
How many different states of the board can Ringo obtain at the end of the process? Find the count modulo .
Two states of the board are considered different when there is a square painted in different colors.
Constraints
- , , and consist of
0and1.
Input
Input is given from Standard Input in the following format:
Output
Print the number of the different states of the board Ringo can obtain at the end of the process, modulo .
2 2
10
01
10
01
6
There are six possible states as shown below.
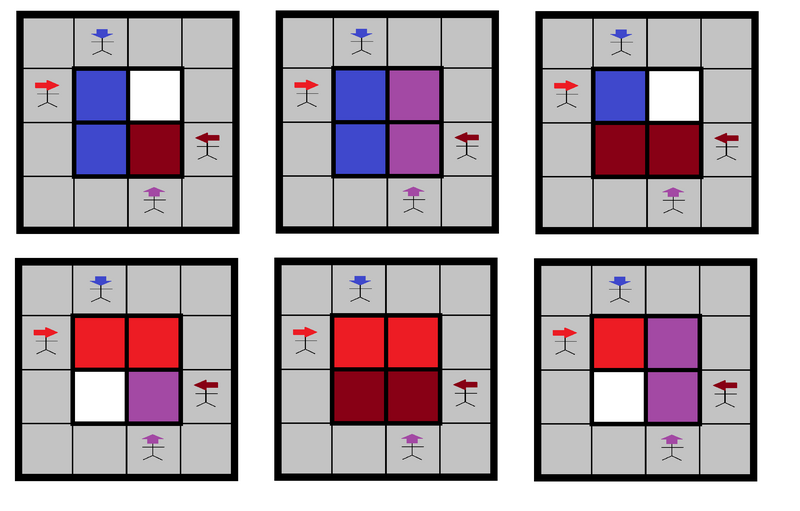
2 2
11
11
11
11
32
3 4
111
111
1111
1111
1276
17 21
11001010101011101
11001010011010111
111010101110101111100
011010110110101000111
548356548
Be sure to find the count modulo .
3 4
000
101
1111
0010
21
9 13
111100001
010101011
0000000000000
1010111111101
177856
23 30
01010010101010010001110
11010100100100101010101
000101001001010010101010101101
101001000100101001010010101000
734524988
