atcoder#ASAPORO2E. Black Cats Deployment
Black Cats Deployment
Score : points
Problem Statement
Snuke Festival 2017 will be held in a tree with vertices numbered . The -th edge connects Vertex and , and has joyfulness .
The staff is Snuke and black cats. Snuke will set up the headquarters in some vertex, and from there he will deploy a cat to each of the other vertices.
For each vertex, calculate the niceness when the headquarters are set up in that vertex. The niceness when the headquarters are set up in Vertex is calculated as follows:
- Let .
- For each integer between and (inclusive) except , do the following:- Add to , where is the smallest joyfulness of an edge on the path from Vertex to Vertex .
- Add to , where is the smallest joyfulness of an edge on the path from Vertex to Vertex .
- The niceness is the final value of .
Constraints
- The given graph is a tree.
- All input values are integers.
Partial Scores
- In the test set worth points, .
- In the test set worth points, .
Input
Input is given from Standard Input in the following format:
Output
Print lines. The -th line must contain the niceness when the headquarters are set up in Vertex .
3
1 2 10
2 3 20
20
30
30
- The figure below shows the case when headquarters are set up in each of the vertices , and .
- The number on top of an edge denotes the joyfulness of the edge, and the number below an vertex denotes the smallest joyfulness of an edge on the path from the headquarters to that vertex.
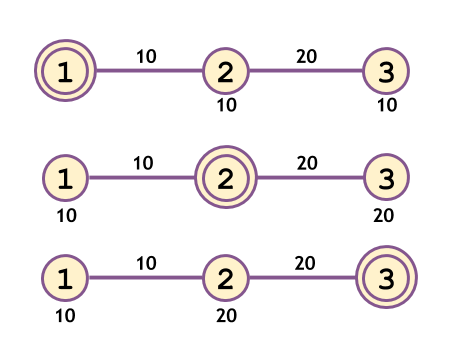
15
6 3 2
13 3 1
1 13 2
7 1 2
8 1 1
2 8 2
2 12 2
5 2 2
2 11 2
10 2 2
10 9 1
9 14 2
4 14 1
11 15 2
16
20
15
14
20
15
16
20
15
20
20
20
16
15
20
19
19 14 48
11 19 23
17 14 30
7 11 15
2 19 15
2 18 21
19 10 43
12 11 25
3 11 4
5 19 50
4 11 19
9 12 29
14 13 3
14 6 12
14 15 14
5 1 6
8 18 13
7 16 14
103
237
71
263
370
193
231
207
299
358
295
299
54
368
220
220
319
237
370
