题目描述

二次元平面上に配置された $N$ 個の点 $(x_i,y_i)$ が与えられます。 $N$ 点の部分集合 $S$ であって、凸多角形をなすものを考えます。 ここで点集合$S$が凸多角形をなすとは、 頂点の集合が $S$ と一致するような正の面積の凸多角形が存在することとします。ただし、凸多角形の内角は全て $180°$ 未満である必要があります。

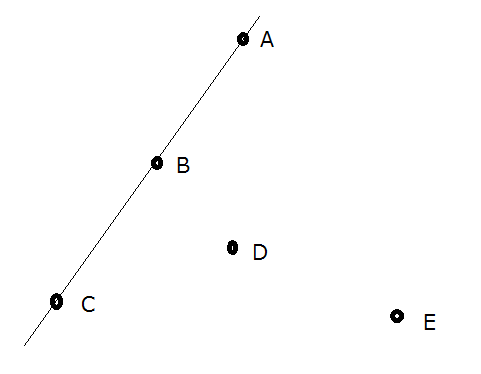
例えば下図では、$S$ として {$A,C,E$}, {$B,D,E$} などは認められますが、{$A,C,D,E$}, {$A,B,C,E$}, {$A,B,C$}, {$D,E$}, {} などは認められません。

$S$ に対し、$N$ 個の点のうち $S$ の凸包の内部と境界 (頂点も含む) に含まれる点の個数を $n$ とおき、 $S$ のスコアを、$2^{n-|S|}$ と定義します。

凸多角形をなすような考えうる全ての $S$ に対してスコアを計算し、これらを足し合わせたものを求めてください。

ただし答えはとても大きくなりうるので、$998244353$ で割った余りをかわりに求めてください。

输入格式

入力は以下の形式で標準入力から与えられる。

$N$ $x_1$ $y_1$ $x_2$ $y_2$ $:$ $x_N$ $y_N$

输出格式

スコアの総和を $998244353$ で割った余りを出力せよ。

题目大意

给定平面上 $N$ 个点的坐标 $x_i,y_i$。从这 $N$ 个点中选出一些可以形成凸包的点，构成点集 $S$ 。点集 $S$ 形成的凸包是指存在顶点的集合与 $S$中的点一致的正面积的凸多边形。但是，凸多边形的内角必须全部不足180°。

例如图中，点集 { $A,C,E$ }, { $B,D,E$ } 即为可以构成凸包的集合，而 { $A,C,D,E$ }, { $A,B,C,E$ }, { $A,B,C$ }, { $D,E$ }, $\varnothing$ 都是不能构成凸包的点集。

对于选出来的集合 $S$，在 $N$ 个点中，将 $S$ 形成的凸包的内部和边上(包括顶点)包含的点的个数设为 $n$，将 $S$ 的贡献定义为$2^{n-|S|}$。

请计算 $N$ 个点能选出的所有集合 $S$ 能构成的凸包的贡献和。

但是，由于答案可能会变得非常大，所以请将贡献和对 $998244353$ 取模。

4
0 0
0 1
1 0
1 1

5

5
0 0
0 1
0 2
0 3
1 1

11

1
3141 2718

0

提示

制約

• $1\ <\ =N\ <\ =200$
• $0\ <\ =x_i,y_i\ <\ 10^4\ (1\ <\ =i\ <\ =N)$
• $i≠j$ なら $x_i≠x_j$ または $y_i≠y_j$
• $x_i,y_i$ は整数

Sample Explanation 1

$S$ として三角形（をなす点集合）が $4$ つと四角形が $1$ つとれます。どれもスコアは $2^0=1$ となるので、答えは $5$ です。

Sample Explanation 2

スコア $1$ の三角形が $3$ つ、スコア $2$ の三角形が$2$つ、スコア $4$ の三角形が $1$ つあるので、答えは $11$ です。

Sample Explanation 3

$S$ として考えられるものがないので、答えは $0$ です。