题目描述

$2$ 次元平面上に $x$ 軸と平行な直線が $m$ 本と $y$ 軸と平行な直線が $n$ 本引いてあります。 $x$ 軸と平行な直線のうち下から $i$ 番目は $y\ =\ y_i$ で表せます。 $y$ 軸と平行な直線のうち左から $i$ 番目は $x\ =\ x_i$ で表せます。

この中に存在しているすべての長方形についてその面積を求め、 合計を $10^9+7$ で割ったあまりを出力してください。

つまり、$1\leq\ i\ <\ j\leq\ n$ と $1\leq\ k\ <\ l\leq\ m$ を満たすすべての組 $(i,j,k,l)$ について、 直線 $x=x_i$, $x=x_j$, $y=y_k$, $y=y_l$ で囲まれる 長方形の面積を求め、合計を $10^9+7$ で割ったあまりを出力してください。

输入格式

入力は以下の形式で標準入力から与えられる。

$n$ $m$ $x_1$ $x_2$ $...$ $x_n$ $y_1$ $y_2$ $...$ $y_m$

输出格式

長方形の面積の合計を $10^9+7$ で割ったあまりを $1$ 行に出力せよ。

题目大意

给定 $n$ 条平行于 $y$ 轴的直线 $x_{1...n}$，和 $m$ 条平行于 $x$ 轴的直线 $y_{1...n}$，

计算 $x_i,x_j$ 和 $y_k,y_l$ 组成的矩形面积之和，$1\le x<y\le n$，$1\le k<l\le m$。

3 3
1 3 4
1 3 6

60

6 5
-790013317 -192321079 95834122 418379342 586260100 802780784
-253230108 193944314 363756450 712662868 735867677

835067060

提示

制約

• $2\ \leq\ n,m\ \leq\ 10^5$
• $-10^9\ \leq\ x_1\ <\ ...\ <\ x_n\ \leq\ 10^9$
• $-10^9\ \leq\ y_1\ <\ ...\ <\ y_m\ \leq\ 10^9$
• $x_i,\ y_i$ は整数である。

Sample Explanation 1

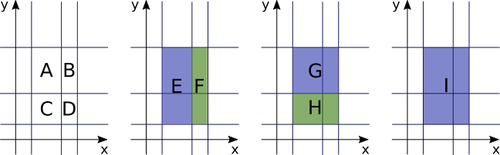
この入力を図にすると、以下のようになります。  長方形 A,B,...,I それぞれの面積を合計すると $60$ になります。