atcoder#AGC058C. [AGC058C] Planar Tree
[AGC058C] Planar Tree
题目描述
ある円環上に 個の頂点が並んでいます. 頂点には時計回りに から の番号がついており,頂点 には整数 が書かれています. ここで, は のいずれかです. また は をそれぞれ つ以上含みます.
これらの 個の頂点を結ぶ辺を 本追加し,木を作ることを考えます. ただしこの時,以下の条件を満たす必要があります.
- 頂点 が直接辺で結ばれているならば, である.
- 追加した辺を線分として描いた時,どの つも端点以外で交わらない.
例えば,以下の図は条件を満たす木の例です.
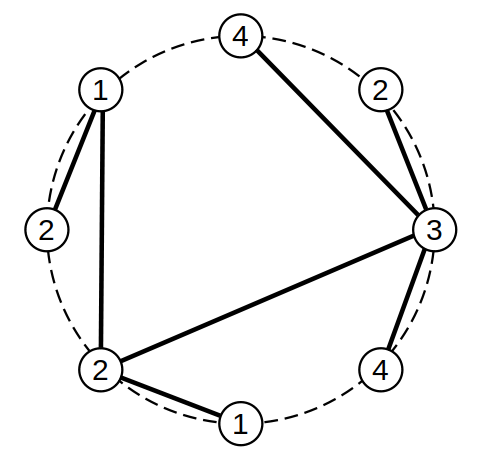
条件を満たすような木を作ることが可能かどうか判定してください.
つの入力ファイルにつき, 個のテストケースを解いてください.
输入格式
入力は以下の形式で標準入力から与えられる.
各ケースは以下の形式で与えられる.
输出格式
各ケースに対し,条件を満たす木を作ることができるならば Yes を,できないならば No を出力せよ.
题目大意
有 组数据 。
每组数据输入一个环,环上的点的个数为 ,并且环上每个点有一个权值 ,保证每种权值都至少出现一次。环上两个点 之间能连边当且仅当 。
问是否可能连上 条边后形成一棵树,且树上每条边不在非端点处相交。
3
4
1 2 3 4
4
1 3 4 2
4
1 4 2 3
Yes
Yes
No
3
8
4 2 3 4 1 2 2 1
8
3 2 2 3 1 3 3 4
8
2 3 3 2 1 4 1 4
Yes
Yes
No
提示
制約
- は をそれぞれ つ以上含む
- つの入力ファイルにつき, の総和は を超えない
- 入力はすべて整数である
Sample Explanation 2
最初のテストケースは,問題文中の図に対応しています.
