题目描述
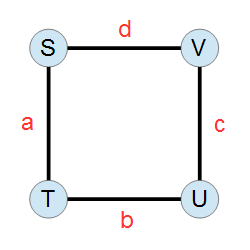
以下の無向グラフにおいて、S から S へのウォークであって辺 ST, TU, UV, VS をそれぞれ a, b, c, d 回通るもの (向きは不問) の数を 998,244,353 で割った余りを求めてください。
输入格式
入力は標準入力から以下の形式で与えられる。
a b c d
输出格式
答えを出力せよ。
题目大意
有一张 4 个点 4 条边的简单无向连通图,点的编号分别为 1,2,3,4 ,边分别连接着 e1:(1,2),e2:(2,3),e3:(3,4),e4:(4,1)。
给定 4 个数 v1,v2,v3,v4 求满足以下条件的路径数量:
从 1 号点出发并到 1 号点结束,且经过第 i 条边 ei 恰好 vi 次。
你需要输出路径数对 998244353 取模的结果。
v1,v2,v3,v4≤5×105
2 2 2 2
10
1 2 3 4
0
470000 480000 490000 500000
712808431
提示
注記
S から S へのウォークとは、頂点の列 v0 = S, v1, …, vk = S であって、各 i (0 ≤ i < k) について vi と vi+1 を結ぶ辺があるものをいいます。 2 つのウォークは、列として異なるときに異なるとみなされます。
制約
- 1 ≤ a, b, c, d ≤ 500,000
- 入力中の全ての値は整数である。
Sample Explanation 1
条件を満たすウォークは 10 個あり、その一例は S → T → U → V → U → T → S → V → S です。

