题目描述

下図のように，$1$ 辺が $N$ 個の点からなる正三角形状に，$N(N+1)/2$ 個の点が並んでいます． 上から $i$ 段目の左から $j$ 番目の点を $(i,\ j)$ で表すことにします($1\ \leq\ i\ \leq\ N$, $1\ \leq\ j\ \leq\ i$)． また，$(i+1,\ j)$ を $(i,\ j)$ のすぐ左下の点，$(i+1,\ j+1)$ を $(i,\ j)$ のすぐ右下の点と呼ぶことにします．

高橋君は，この点を結んで，$M$ 個の折れ線 $1,\ 2,\ ...,\ M$ を描くことにしました． 各折れ線は，$(1,\ 1)$ から始めて，「現在いる点のすぐ左下の点かすぐ右下の点を選び，現在いる点と選んだ点を直線で結んだのち，選んだ点へ移動する」 ことを $N-1$ 回繰り返すことで得られます． すなわち，ある $X_{i,1},\ ...,\ X_{i,N}$ が存在して，次が成り立ちます：

• 折れ線 $i$ は，$N$ 個の点 $ (1,\ X_{i,1}),\ (2,\ X_{i,2}),\ ...,\ (N,\ X_{i,N}) $ をこの順で結んでいる．
• $j=1,\ 2,\ ...,\ N-1$ に対して，$X_{i,j+1}\ =\ X_{i,j}$ または $X_{i,j+1}\ =\ X_{i,j}+1$ が成り立つ．

高橋君は，折れ線 $i+1$ が折れ線 $i$ の左に来ることはないように折れ線を描きたいです． つまり，$j=1,\ 2,\ ...,\ N$ に対して，$X_{1,j}\ \leq\ X_{2,j}\ \leq\ ...\ \leq\ X_{M,j}$ が成り立ちます．

また，高橋君は，折れ線の曲がり方について $K$ 個の条件を満たすように折れ線を描かなければなりません． $i$ 番目の条件は $(A_i,\ B_i,\ C_i)$ で表され，これは次を意味します：

• $C_i=0$ のときは，折れ線 $A_i$ を描くとき，$B_i$ 回目の移動においては，その時いる点のすぐ左下の点を選ぶ．
• $C_i=1$ のときは，折れ線 $A_i$ を描くとき，$B_i$ 回目の移動においては，その時いる点のすぐ右下の点を選ぶ．

すなわち，$X_{A_i,\ {B_i}+1}\ =\ X_{A_i,\ B_i}\ +\ C_i$ を意味します．

高橋君が $M$ 個の折れ線を描く方法が何通りあるかを mod $1000000007$ で求めてください．

输入格式

入力は以下の形式で標準入力から与えられる。

$N$ $M$ $K$ $A_1$ $B_1$ $C_1$ $A_2$ $B_2$ $C_2$ : $A_K$ $B_K$ $C_K$

输出格式

高橋君が $M$ 個の折れ線を描く方法は何通りあるかを mod $1000000007$ で出力せよ．

题目大意

• 给定一个 $N$ 层的三角形图，第 $i$ 层有 $i$ 个节点。
• 第 $i$ 层的节点，从左到右依次标号为 $(i, 1), (i, 2), \ldots , (i, i)$（具体如上图所示）。
• 你需要从 $(1, 1)$ 往下画 $M$ 条折线。
• 对于每条折线的每一个小段，你可以从 $(i, j)$ 画到 $(i + 1, j)$ 或者 $(i + 1, j + 1)$。
• 同时你还必须保证第 $i$ 条折线的任何一个位置必须不能处在第 $i - 1$ 条折线的左侧，它们必须按照从左到右的顺序排列。
• 有 $K$ 条限制，每条限制形如 $(A_i, B_i, C_i)$。
• 表示第 $A_i$ 条折线处于位置 $(B_i, j)$ 时，下一小段必须走向 $(B_i + 1, j + C_i)$，也就是当 $C_i = 0$ 时向左，当 $C_i = 1$ 时向右。
• 询问不同的折线画法的方案数，对 ${10}^9 + 7$ 取模。
• $1 \le N, M \le 20$，$0 \le K \le M (N - 1)$。其它变量在合理范围内。

3 2 1
1 2 0

6

3 2 2
1 1 1
2 1 0

0

5 4 2
1 3 1
4 2 0

172

20 20 0

881396682

提示

注意

提出を行う前に，「コードテスト」を利用して実行時間を計測することを強く推奨する．

制約

• $1\ \leq\ N\ \leq\ 20$
• $1\ \leq\ M\ \leq\ 20$
• $0\ \leq\ K\ \leq\ (N-1)M$
• $1\ \leq\ A_i\ \leq\ M$
• $1\ \leq\ B_i\ \leq\ N-1$
• $C_i\ =\ 0,1$
• $(A_i,\ B_i)$ として同じ組は複数回与えられない．

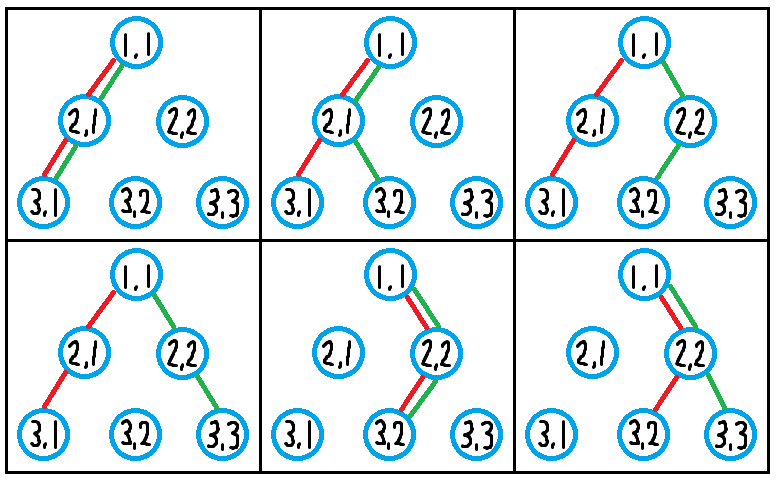
Sample Explanation 1

下図に示すように，$6$ 通りの描き方があります．ただし，赤線は折れ線 $1$，緑線は折れ線 $2$ を表します：