Score : $1600$ points

Problem Statement

There is a directed graph $G$ with $N$ vertices and $M$ edges. The vertices are numbered $1$ through $N$, and the edges are numbered $1$ through $M$. Edge $i$ is directed from $x_i$ to $y_i$. Here, $x_i < y_i$ holds. Also, there are no multiple edges in $G$.

Consider selecting a subset of the set of the $M$ edges in $G$, and removing these edges from $G$ to obtain another graph $G'$. There are $2^M$ different possible graphs as $G'$.

Alice and Bob play against each other in the following game played on $G'$. First, place two pieces on vertices $1$ and $2$, one on each. Then, starting from Alice, Alice and Bob alternately perform the following operation:

• Select an edge $i$ such that there is a piece placed on vertex $x_i$, and move the piece to vertex $y_i$ (if there are two pieces on vertex $x_i$, only move one). The two pieces are allowed to be placed on the same vertex.

The player loses when he/she becomes unable to perform the operation. We assume that both players play optimally.

Among the $2^M$ different possible graphs as $G'$, how many lead to Alice's victory? Find the count modulo $10^9+7$.

Constraints

• $2 \leq N \leq 15$
• $1 \leq M \leq N(N-1)/2$
• $1 \leq x_i < y_i \leq N$
• All $(x_i,\ y_i)$ are distinct.

Input

Input is given from Standard Input in the following format:

$N$ $M$

$x_1$ $y_1$

$x_2$ $y_2$

$:$

$x_M$ $y_M$

Output

Print the number of $G'$ that lead to Alice's victory, modulo $10^9+7$.

2 1
1 2

1

The figure below shows the two possible graphs as $G'$. A graph marked with ○ leads to Alice's victory, and a graph marked with × leads to Bob's victory.

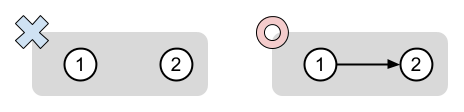
3 3
1 2
1 3
2 3

6

The figure below shows the eight possible graphs as $G'$.

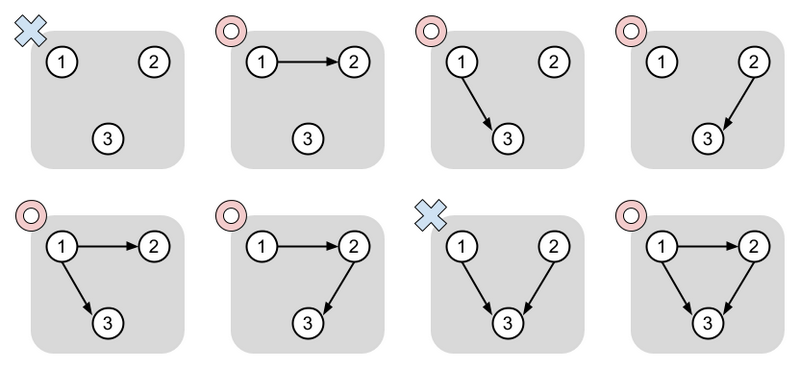
4 2
1 3
2 4

2

5 10
2 4
3 4
2 5
2 3
1 2
3 5
1 3
1 5
4 5
1 4

816