atcoder#AGC013E. [AGC013E] Placing Squares
[AGC013E] Placing Squares
题目描述
joisinoお姉ちゃんは、長さ の棒を持っています。 この棒には 個の印がついています。 個目の印は、棒の左端から距離 の位置についています。
joisinoお姉ちゃんは、この棒の上にいくつかの正方形を置くことにしました。 正方形を置くにあたって、以下のような条件があります。
- 辺の長さが整数の正方形しか置いてはならない。
- 全ての正方形は、底辺が棒と接するように置かなくてはならない。
- 正方形は、棒の上に敷き詰められている必要がある。 つまり、正方形が棒からはみ出したり、上に正方形が乗っていないような棒の部分が存在したりしてはならない。
- 棒の印がついている部分の真上は、 つの正方形の境目であってはならない。
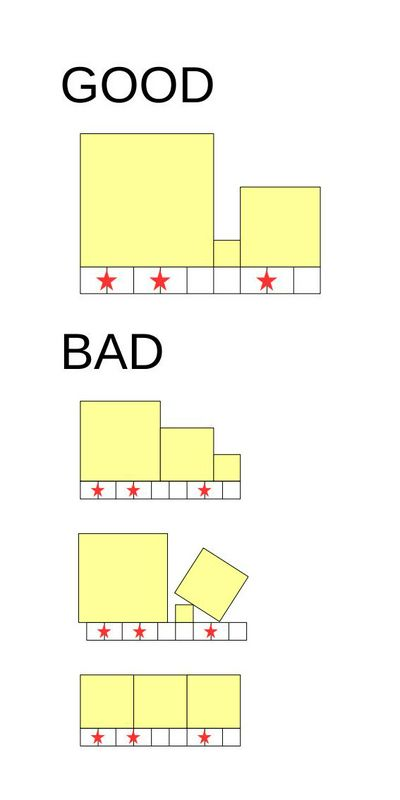 条件を満たす配置とそうでない配置の例
条件を満たす配置とそうでない配置の例
ある正方形の配置の美しさとは、置かれている正方形の面積をすべて掛け合わせた値です。 joisinoお姉ちゃんは、上の条件を満たすような正方形の配置全てについて、その美しさを求め、その総和を知りたくなりました。 あなたの仕事は、joisinoお姉ちゃんの代わりにこれを求めるプログラムを作ることです。 なお、答えは非常に大きくなることがあるので、 で割った余りを出力してください。
输入格式
入力は以下の形式で標準入力から与えられる。
输出格式
あり得る正方形の配置全てについて、その美しさを求め、その総和を で割った余りを出力せよ。
题目大意
给定一个长度为 的木板,木板上有 个标记点,距离木板左端点的距离分别为 ,现在你需要在木板上放置一些不相交正方形,正方形需要满足
-
正方形的边长为整数
-
正方形底面需要紧贴木板
-
正方形不能超出木板,正方形要将所有的木板覆盖
-
标记点的位置不能是两个正方形的交界处
下面是一些满足条件与不满足条件的例子
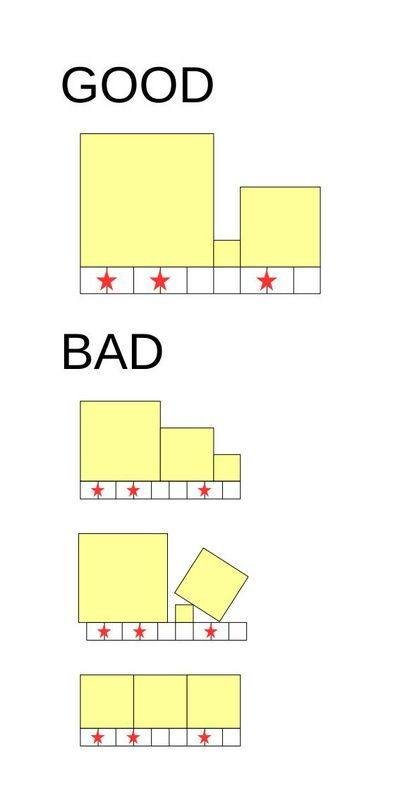
一种合法的正方形放置方案的贡献为所有正方形面积的乘积,也就是为 , 为正方形的边长。
请你求出所有合法方案的贡献之和,答案对 取模。
,。
3 1
2
13
5 2
2 3
66
10 9
1 2 3 4 5 6 7 8 9
100
1000000000 0
693316425
提示
制約
- 入力は全て整数である
- $1\ \leq\ X_1\ <\ X_2\ <\ ...\ <\ X_{M-1}\ <\ X_M\ \leq\ N-1$
Sample Explanation 1
可能な配置は、 - 一辺の長さ の正方形を左に、一辺の長さ の正方形を右に置く - 一辺の長さ の正方形を置く の 通りで、その美しさの合計は、$(1\ \times\ 1\ \times\ 2\ \times\ 2)\ +\ (3\ \times\ 3)\ =\ 13$ となります。
