atcoder#AGC007C. [AGC007C] Pushing Balls
[AGC007C] Pushing Balls
题目描述
個の球と 個の穴が一直線上に並んでいます。球には左から順に から の番号が、穴には左から順に から の番号が振られています。 番の球は 番の穴と 番の穴の間に置かれており、隣り合う穴と球の間の距離を左から順に並べて得られる数列を () とおきます。 の値とパラメータ が与えられており、 が任意の () に対して成り立っています。
これら 個の球を 個ずつ転がし、穴に落としていくことを考えます。球が穴の上を通ると、その穴にすでに別の球が入っていなければその穴に落ちます。すでに別の球がその穴に入っていた場合は、球は落ちずにそのまま転がり続けます。(なお、この問題で考える球の転がし方において、球どうしが衝突することはありません。)
球を転がす際は、まだ転がされていない球の中から等確率で つを選び、その球を左または右に等確率で転がします。これを 回繰り返してすべての球を転がすとき、すべての球が移動する距離の総和の期待値を求めてください。
以下に , , の場合の球の転がし方の例を挙げます。
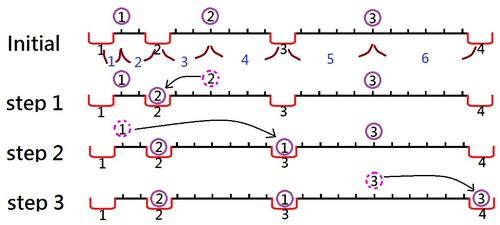
- 番の球を左に転がす。球は 番の穴に落ちる。球が移動する距離は である。
- 番の球を右に転がす。球は 番の穴の上を通り、 番の穴に落ちる。球が移動する距離は である。
- 番の球を右に転がす。球は 番の穴に落ちる。球が移動する距離は である。
この例では、球が移動する距離の総和は となります。
なお、球をどのように転がしてもどの球も必ずいずれかの穴に落ち、最後に穴が一つだけ空のまま残ることになります。
输入格式
入力は以下の形式で標準入力から与えられる。
输出格式
答えを小数で出力せよ。絶対誤差または相対誤差のいずれかが 以内でなければならない。
题目大意
在一条直线上有 个球和 个洞。记每个球与相邻的洞的距离为 且 。
要将 个球均推入洞中。当球滚过洞时,如果洞中还没有球,球将掉入洞中。否则,球将继续滚动。
每次会随机选择任一未进洞的球,并随机选择一个方向推球。
给定 ,求出在不发生碰撞的情况下,每个球移动距离的期望(误差小于 )。
1 3 3
4.500000000000000
2 1 0
2.500000000000000
1000 100 100
649620280.957660079002380
提示
制約
- 入力値はすべて整数である。
Sample Explanation 1
球が 個、穴が 個あります。球から左の穴までの距離は 、球から右の穴までの距離は です。球を左に転がすか右に転がすかの 通りの転がし方があり、それぞれにおいて球が移動する距離は です。したがって、答えは となります。
