配点 : $1400$ 点

問題文

しぐま君とすぎむ君はゲームをすることにしました。

このゲームは $N$ 頂点のグラフの上で行います。頂点には $1,2,...,N$ と番号がついています。グラフには $N-1$ 本の赤い辺と $N-1$ 本の青い辺があり、どちらも木となっています。赤い辺は $(a_i, b_i)$ で表し、青い辺は $(c_i, d_i)$ で表します。

二人はそれぞれ駒を $1$ 個ずつ持っており、しぐま君の駒の初期位置は頂点 $X$、すぎむ君の駒の初期位置は頂点 $Y$ です。

このゲームはターン制で、ターン $1$, ターン $2$, ターン $3$, ... と進んでいきます。そして、ターン $1, 3, 5, ...$ はしぐま君、ターン $2, 4, 6, ...$ はすぎむ君の手番です。

二人は自分の手番では、自分の駒を動かすかパスをします。ただし動かせる頂点には制限があり、しぐま君は赤い辺、すぎむ君は青い辺で隣り合った頂点のみに駒を動かせます。

もし二つの駒が同じ頂点に来るとその時点でゲームは終了します。そしてターン $i$ での操作の後にゲームが終了したならば、$i$ を総ターン数とします。

しぐま君は総ターン数を出来る限り大きく、すぎむ君は出来る限り小さくしたいです。

二人はこの目的のもとで最適に行動をすると仮定したとき、ゲームは終了するかを判定し、終了する場合は総ターン数はいくつになるか求めてください。

制約

• $2 \leq N \leq 200,000$
• $1 \leq X, Y \leq N$
• $X \neq Y$
• $1 \leq a_i, b_i, c_i, d_i \leq N$
• 赤い辺と青い辺はそれぞれ木である

入力

入力は以下の形式で標準入力から与えられる。

$N$ $X$ $Y$

$a_1$ $b_1$

$a_2$ $b_2$

:

$a_{N-1}$ $b_{N-1}$

$c_1$ $d_1$

$c_2$ $d_2$

:

$c_{N-1}$ $d_{N-1}$

出力

$1$ 行に答えを出力する。 ただし、いつまでもゲームが終了しない場合は -1 を出力する。

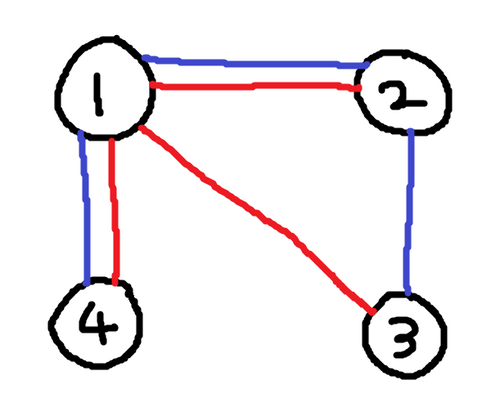
4 1 2
1 2
1 3
1 4
2 1
2 3
1 4

4

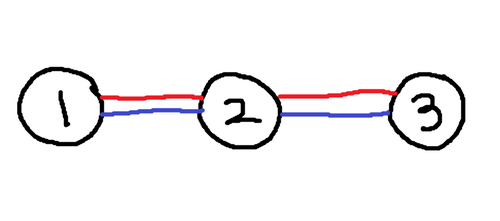
3 3 1
1 2
2 3
1 2
2 3

4

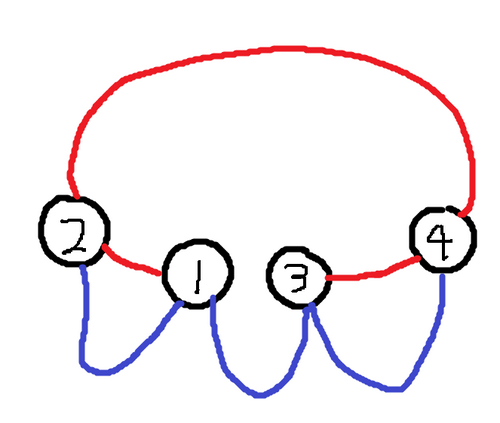
4 1 2
1 2
3 4
2 4
1 2
3 4
1 3

2

4 2 1
1 2
3 4
2 4
1 2
3 4
1 3

-1

5 1 2
1 2
1 3
1 4
4 5
2 1
1 3
1 5
5 4

6