atcoder#AGC004F. [AGC004F] Namori
[AGC004F] Namori
Score : points
Problem Statement
You are given an undirected graph with vertices and edges. Here, holds and the graph is connected. There are no self-loops or multiple edges in this graph.
The vertices are numbered through , and the edges are numbered through . Edge connects vertices and .
The color of each vertex can be either white or black. Initially, all the vertices are white. Snuke is trying to turn all the vertices black by performing the following operation some number of times:
- Select a pair of adjacent vertices with the same color, and invert the colors of those vertices. That is, if the vertices are both white, then turn them black, and vice versa.
Determine if it is possible to turn all the vertices black. If the answer is positive, find the minimum number of times the operation needs to be performed in order to achieve the objective.
Constraints
- There are no self-loops or multiple edges in the given graph.
- The given graph is connected.
Partial Score
- In the test set worth points, .
Input
The input is given from Standard Input in the following format:
Output
If it is possible to turn all the vertices black, print the minimum number of times the operation needs to be performed in order to achieve the objective.
Otherwise, print -1 instead.
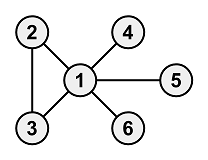
6 5
1 2
1 3
1 4
2 5
2 6
5
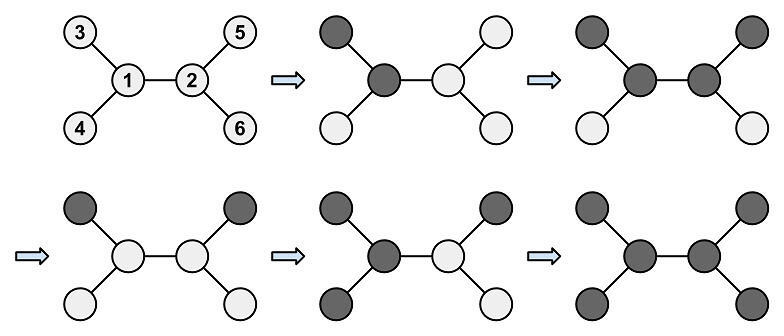
For example, it is possible to perform the operations as shown in the following diagram:
3 2
1 2
2 3
-1
It is not possible to turn all the vertices black.
4 4
1 2
2 3
3 4
4 1
2
This case is not included in the test set for the partial score.
6 6
1 2
2 3
3 1
1 4
1 5
1 6
7
This case is not included in the test set for the partial score.