题目描述

この問題は インタラクティブな問題（あなたが作成したプログラムとジャッジプログラムが標準入出力を介して対話を行う形式の問題）です。

$N$ 個の頂点と $M$ 本の辺からなる連結かつ単純な無向グラフがあります。 頂点には $1$ から $N$ までの整数の番号がついています。

あなたは、はじめ頂点 $1$ にいます。 隣り合う頂点に移動することを最大 $2N$ 回まで繰り返して、頂点 $N$ へ移動してください。

ただし、はじめはグラフの辺をすべて知ることはできず、今いる頂点と隣り合っている頂点の情報を知ることができます。

Input & Output Format

最初に、グラフの頂点数 $N$ と辺数 $M$ を標準入力から受け取ってください。

$N$ $M$

次に、あなたはジャッジに対して問題文中の操作を $2N$ 回まで繰り返すことができます。

各操作のはじめには、あなたが現在いる頂点に隣接する頂点が次の形式で標準入力から与えられます。

$k$ $v\ _\ 1$ $v\ _\ 2$ $\ldots$ $v\ _\ k$

ここで、$v\ _\ i\ (1\leq\ i\leq\ k)$ は $1$ 以上 $N$ 以下の整数で、$v\ _\ 1\lt\ v\ _\ 2\lt\cdots\lt\ v\ _\ k$ を満たします。

あなたは、$v\ _\ i\ (1\leq\ i\leq\ k)$ を $1$ つ選んで以下の形式で標準出力へ出力してください。

$v\ _\ i$

この操作をすることで、あなたは頂点 $v\ _\ i$ へ移動します。

移動回数が $2N$ 回を上回ったり、不正な出力を行った場合、ジャッジは標準入力に -1 を送ります。

移動する先の頂点が頂点 $N$ である場合、ジャッジは標準入力に OK を送り、終了します。

-1 もしくは OK を受け取った場合、ただちにあなたのプログラムを終了させてください。

题目大意

本题为交互题。

给定一张 $N$ 个点（编号为 $1 \sim N$），$M$ 条边的无向连通图，保证无重边无自环，但是起初这张图的所有边是未知的。

起初你在 $1$ 号点。在交互开始或者每次完成操作的时候，交互库会告诉你从当前点出发的边连向哪些点。在此之后，你需要进行一次操作：走到其中的一个点。

你需要执行不超过 $2N$ 次操作到达点 $N$。

以下为交互流程：

1. 首先读入一行两个正整数 $N,M$。
2. 接下来：

• 如果操作次数大于 $2N$ 或者刚刚执行了不合法的操作，交互库会返回 -1 到标准输入中。你需要立即结束程序。
• 否则，如果刚刚执行的操作使得你到达了点 $N$，那么交互库会返回 OK 到标准输入中并结束程序。
• 否则，交互库会返回 $K+1$ 个非负整数到标准输入中：第一个是 $K$，接下来是 $K$ 个互不相同的正整数 $v_1,v_2,\cdots,v_k$，代表从当前点出发的边连向的点的集合。

3. 你需要从其中选择一个 $v_i$ 输出，此后返回到第 2 步直到程序结束。

提示

制約

• $2\leq\ N\leq100$
• $N-1\leq\ M\leq\dfrac{N(N-1)}2$
• グラフは連結かつ単純
• 入力はすべて整数

注意点

• 出力を行うたびに、末尾に改行を入れて標準出力を flush してください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
• 対話の途中で不正な出力を行った、あるいはプログラムが途中で終了した場合のジャッジ結果は不定です。
• 頂点 $N$ に到達したらただちにプログラムを終了してください。そうしない場合、ジャッジ結果は不定です。
• この問題のジャッジはアダプティブです。つまり、制約および以前の出力に矛盾しない範囲でグラフの形が変わる場合があります。

入出力例

以下は、$N=4,M=5$ の場合の入出力例です。 この入出力では、グラフは以下の図のようになっています。

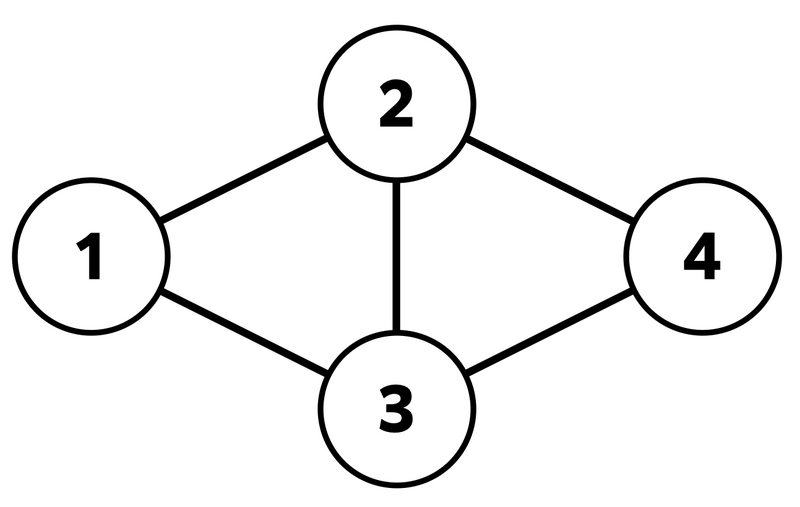
入力 出力 説明     `4 5`  $ N $ と $ M $ が与えられます。   `2 2 3`  はじめ、あなたは頂点 $ 1 $ にいます。頂点 $ 1 $ に隣接している頂点が与えられます。    `3` 移動する頂点として、頂点 $ v\ _\ 2=3 $ を選びます。    `3 1 2 4`  頂点 $ 3 $ に隣接している頂点が与えられます。    `2` 移動する頂点として、頂点 $ v\ _\ 2=2 $ を選びます。    `3 1 3 4`  頂点 $ 2 $ に隣接している頂点が与えられます。    `4` 移動する頂点として、頂点 $ v\ _\ 3=4 $ を選びます。    `OK`  $ 8(=2\times4) $ 回以内で頂点 $ 4 $ に到達したので、`OK` が渡されます。   `OK` を受け取ったあと、ただちにプログラムを終了することで正解と判定されます。