atcoder#ABC286E. [ABC286E] Souvenir
[ABC286E] Souvenir
题目描述
個の都市があり、いくつかの相異なる都市の間は一方通行の直行便によって移動することができます。
どの直行便が存在するかは 個の長さ の文字列 によって表され、 の 文字目が Y のとき都市 から都市 へ向かう直行便が存在することを、 N のとき存在しないことを示します。
また、各都市ではお土産が つずつ売られており、都市 では価値 のお土産が売られています。
次のような問題を考えます。
高橋君は今都市 におり、いくつかの直行便を乗り継いで( とは異なる)都市 に向かおうとしています。
さらに、高橋君は移動する途中で訪れた都市( を含む)において つずつお土産を購入します。
都市 から都市 へ向かう経路が複数存在する時、高橋君は次のような経路で移動することを考えています。
- 都市 から 都市 に向かう経路のうち、使う直行便の数が最小である。
- さらにそのような経路のうち、購入するお土産の価値の総和が最大である。
高橋君が都市 から に直行便を乗り継いで移動することが可能か判定し、 可能な時は高橋君が上の条件をみたすように経路を選んだ時の「使用する直行便の本数」と「お土産の価値の総和」を求めよ。
相異なる都市の組 が 個与えられます。
各 について、 とした時の上記の問題の答えを出力してください。
输入格式
入力は以下の形式で標準入力から与えられる。
输出格式
行出力せよ。
行目には、 都市 から都市 に移動することが不可能な時は Impossible を、 可能な時は上記のように経路を選んだ時の「使用する直行便の本数」と「お土産の価値の総和」をこの順に空白区切りで出力せよ。
题目大意
题目描述
从前有 座岛,每个岛上有 个金币,各个岛间有若干条单向航线相连。
你从某个岛开始旅行,经过一个岛(包括最开始所在的岛)就会拿走上面的金币。
现在问你 个问题:从岛 旅行到岛 ,最少要走几条航线,以及恰好走这么多条航线最多能获得多少金币。如果根本无法到达 ,输出 Impossible。
询问之间相互独立。
输入格式
输入第一行一个整数 表示岛的数量。
接下来一行 个整数表示每个岛上的金币数。
接下来 行每行一个长为 的字符串,第 行字符串的第 个字符若为 Y 则表示岛 和 间有单向航线,否则表示没有。
接下来一行一个整数 表示询问次数。
最后 行每行两个整数 ,询问你从岛 旅行到岛 最少要走几条航线,以及恰好走这么多条航线最多能获得多少金币。
输出格式
对于每个询问输出一行:
- 若 不能到达 ,输出
Impossible; - 否则,输出从岛 旅行到岛 最少要走几条航线,以及恰好走这么多条航线最多能获得多少金币。
样例解释 1
这些岛的结构如下:
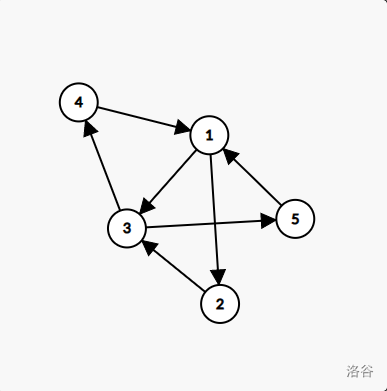
- 对于第 个询问,因为岛 有一条航线通往岛 ,显然最少航线为 条,此时能拿到岛 和岛 上的金币共 个。
- 对于第 个询问,可以证明最少航线为 条,有两种方案 和 ,总金币分别为 和 ,故最多金币为 。
- 对于第 个询问,只有一种方案 可以使航线数最少为 ,所得金币为 。
样例解释 2
笑死,连航线都没有。
数据范围与约定
对于 的数据,$2\le n\le 300,1\le a_i\le 10^9,1\le q\le n(n-1),1\le u_i,v_i\le n$,且询问中的 各不相同。
翻译者:not_Rick_Astley
5
30 50 70 20 60
NYYNN
NNYNN
NNNYY
YNNNN
YNNNN
3
1 3
3 1
4 5
1 100
2 160
3 180
2
100 100
NN
NN
1
1 2
Impossible
提示
制約
- は
YとNのみからなる長さ の文字列 - の 文字目は
N - ならば
- は全て整数
Sample Explanation 1
の時について、都市 から都市 への直行便が存在するため、 使用する直行便としてあり得る最小の値はその直行便を使用した時の 本となります。 この時、お土産の価値の総和は となります。 の時について、使用する直行便としてあり得る最小の値は 本で、 最小値を達成する経路としては都市 と都市 の 通りが考えられます。 それぞれの経路の時のお土産の価値の総和は , なので、 高橋君は後者の経路を選び、この時お土産の価値の総和は となります。 の時について、都市 と進んだ時に使用する直行便の本数は最小となり、 この時お土産の価値の総和は となります。
Sample Explanation 2
直行便が全く存在しないこともあります。
