atcoder#ABC267B. [ABC267B] Split?
[ABC267B] Split?
题目描述
ボウリングのピンは から の番号が付けられており、上から見ると下図のように配置されます。
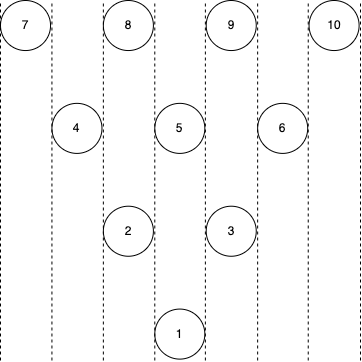
この図の二つの点線に挟まれた部分を列と呼ぶことにします。
例えば、ピン とピン はそれぞれ同じ列に存在します。
いくつかのピンが倒れた状態のうち、特殊なものはスプリットと呼ばれます。
ピンの配置がスプリットであるとは、以下の条件が全て成り立つことを言います。
- ピン が倒れている。
- ある二つの異なる列であって、次の条件を満たすものが存在する。
- それぞれの列には、立っているピンが 本以上存在する。
- それらの列の間に、ピンが全て倒れている列が存在する。
具体例は入出力例を参考にしてください。
さて、あるピンの配置が長さ の文字列 として与えられます。 について、ピン が倒れているとき の 文字目は 0 であり、ピン が立っているとき の 文字目は 1 です。
で表されるピンの配置がスプリットかどうか判定してください。
输入格式
入力は以下の形式で標準入力から与えられる。
输出格式
で表されるピンの配置がスプリットなら Yes を、そうでないなら No を出力せよ。
0101110101
Yes
0100101001
Yes
0000100110
No
1101110101
No
提示
制約
- は
0と1からなる長さ の文字列
Sample Explanation 1
倒れているピンを灰色で、立っているピンを白色で示すと下図のようになります。  ピン が立っている列とピン が立っている列の間にはピン が置かれている列が存在しますが、ピン はいずれも倒れているので、この配置はスプリットです。
Sample Explanation 2

Sample Explanation 3
 この配置はスプリットではありません。
Sample Explanation 4
 ピン が倒れていないので、スプリットではありません。
