题目描述

無限に広がる $2$ 次元グリッドがあり、マス $(r_1,\ c_1)$ に駒「超竜馬」が置かれています。
この駒は、 $1$ 手で次のような動きができます。

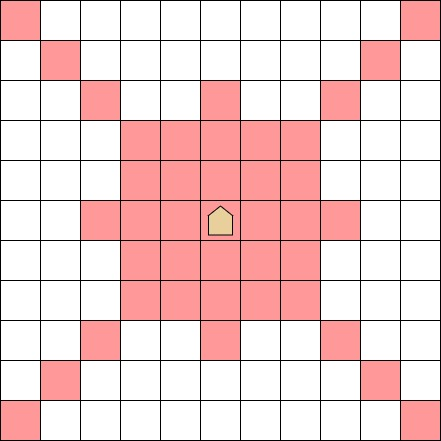
より正確には、超竜馬がマス $(a,\ b)$ にあるとき、以下のいずれかの条件を満たすマス $(c,\ d)$ に動かすことができます。

• $a\ +\ b\ =\ c\ +\ d$
• $a\ -\ b\ =\ c\ -\ d$
• $|a\ -\ c|\ +\ |b\ -\ d|\ \le\ 3$

超竜馬を $(r_1,\ c_1)$ から $(r_2,\ c_2)$ に動かすのに必要な最小手数を求めてください。

输入格式

入力は以下の形式で標準入力から与えられる。

$r_1$ $c_1$ $r_2$ $c_2$

输出格式

超竜馬を $(r_1,\ c_1)$ から $(r_2,\ c_2)$ に動かすのに必要な最小手数を出力せよ。

题目大意

有一个无限大的棋盘，棋盘上的点 $(a,b)$ 能一步走到 $(b,c)$，当且仅当下面的三条条件至少一条成立：

• $a+b=c+d$
• $a-b=c-d$
• $|a-c|+|b-d|\le 3$

求 $(r_1,c_1)$ 走到 $(r_2,c_2)$ 的最少步数。

1 1
5 6

2

1 1
1 200001

2

2 3
998244353 998244853

3

1 1
1 1

0

提示

制約

• 入力は全て整数
• $1\ \le\ r_1,\ c_1,\ r_2,\ c_2\ \le\ 10^9$

Sample Explanation 1

例えば、 $ (1,\ 1)\ \rightarrow\ (5,\ 5)\ \rightarrow\ (5,\ 6) $ と動かすと $2$ 手になります。

Sample Explanation 2

例えば、 $ (1,\ 1)\ \rightarrow\ (100001,\ 100001)\ \rightarrow\ (1,\ 200001) $ と動かすと $2$ 手になります。

Sample Explanation 3

例えば、 $ (2,\ 3)\ \rightarrow\ (3,\ 3)\ \rightarrow\ (-247,\ 253)\ \rightarrow\ (998244353,\ 998244853) $ と動かすと $3$ 手になります。