100 atcoder#ABC054C. [ABC054C] One-stroke Path
[ABC054C] One-stroke Path
题目描述
自己ループと二重辺を含まない 頂点 辺の重み無し無向グラフが与えられます。
番目の辺は頂点 と頂点 を結びます。
ここで、自己ループは となる辺のことを表します。
また、二重辺は かつ となる辺のことを表します。
頂点 を始点として、全ての頂点を1度だけ訪れるパスは何通りありますか。
ただし、パスの始点と終点の頂点も訪れたものとみなします。
例として、図1のような無向グラフが与えられたとします。
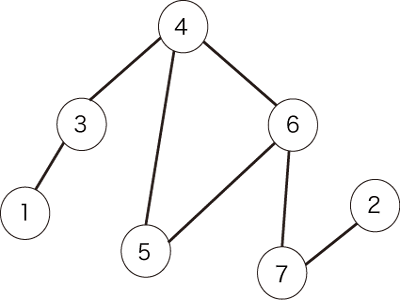 図1:無向グラフの例
図1:無向グラフの例
このとき、図2で表されるパスは条件を満たします。
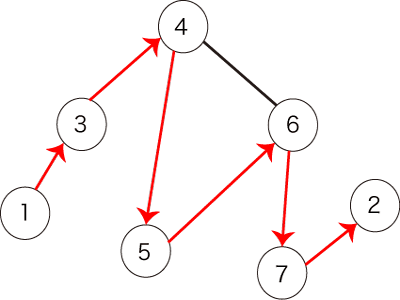 図2:条件を満たすパスの例
図2:条件を満たすパスの例
しかし、図3で表されるパスは条件を満たしません。全ての頂点を訪れていないからです。
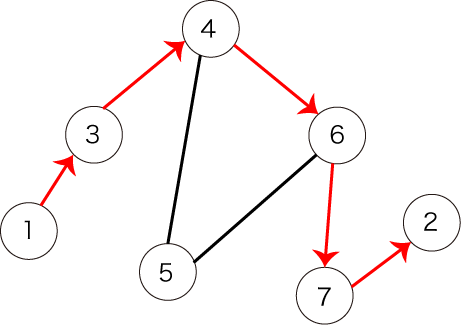 図3:条件を満たさないパスの例1
図3:条件を満たさないパスの例1
また、図4で表されるパスも条件を満たしません。始点が頂点 ではないからです。
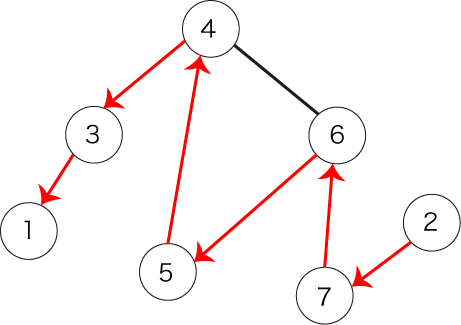 図4:条件を満たさないパスの例2
図4:条件を満たさないパスの例2
输入格式
入力は以下の形式で標準入力から与えられる。
输出格式
問題文の条件を満たすパスが何通りあるか出力せよ。
题目大意
题目描述
给定一个没有重边和自环的 个点 条边的无权无向图,第 条边连接顶点 和 。
求以顶点 为起点,只访问 次所有顶点的路径有多少条?特别地,起点和终点也视为被访问。
输入格式
第一行两个整数 。
接下来 行,其中第 行两个整数 。
$N M \\ a _ 1 b _ 1 \\ a _ 2 b _ 2 \\ \kern {0.667 em} \vdots \\ a _ M b _ M$
输出格式
输出满足条件的路径有多少。
数据范围
$2 \le N \le 8 \\ 0 \le M \le N(N - 1) \\ 1 \le a _ i < b _ i \le N$
给定的无向图中不包含重边和自环。
3 3
1 2
1 3
2 3
2
7 7
1 3
2 7
3 4
4 5
4 6
5 6
6 7
1
提示
制約
- 与えられるグラフは自己ループと二重辺を含まない。
Sample Explanation 1
与えられるグラフは以下の図で表されます。 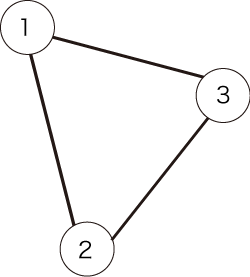 条件を満たすパスは以下の 通りです。 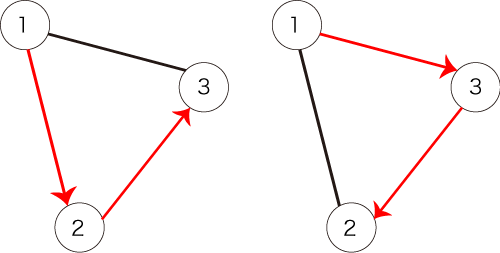
Sample Explanation 2
このテストケースは問題文の例と同じです。
