配点 : $300$ 点

問題文

自己ループと二重辺を含まない $N$ 頂点 $M$ 辺の重み無し無向グラフが与えられます。 $i (1 \leq i \leq M)$ 番目の辺は頂点 $a_i$ と頂点 $b_i$ を結びます。 ここで、自己ループは $a_i = b_i (1 \leq i \leq M)$ となる辺のことを表します。 また、二重辺は $a_i=a_j$ かつ $b_i=b_j (1 \leq i となる辺のことを表します。 頂点 $1$ を始点として、全ての頂点を1度だけ訪れるパスは何通りありますか。 ただし、パスの始点と終点の頂点も訪れたものとみなします。

例として、図1のような無向グラフが与えられたとします。

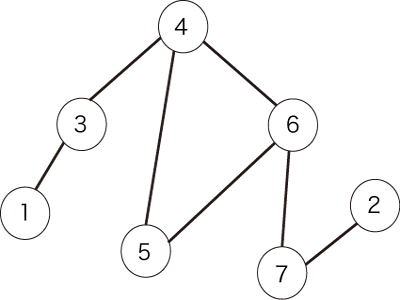
図1：無向グラフの例

このとき、図2で表されるパスは条件を満たします。

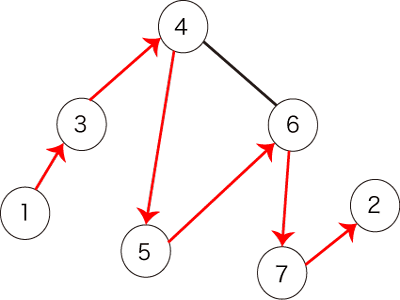
図2：条件を満たすパスの例

しかし、図3で表されるパスは条件を満たしません。全ての頂点を訪れていないからです。

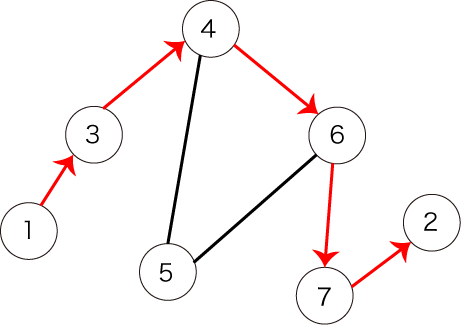
図3：条件を満たさないパスの例1

また、図4で表されるパスも条件を満たしません。始点が頂点 $1$ ではないからです。

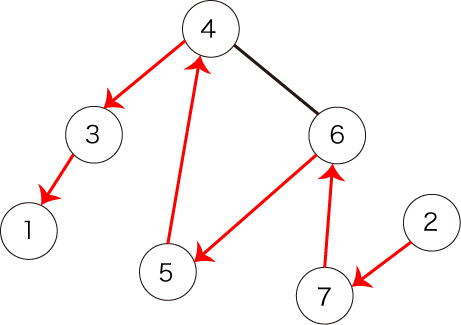
図4：条件を満たさないパスの例2

制約

• $2 \leq N \leq 8$
• $0 \leq M \leq N(N-1)/2$
• $1 \leq a_i
• 与えられるグラフは自己ループと二重辺を含まない。

入力

入力は以下の形式で標準入力から与えられる。

$N$ $M$

$a_1$ $b_1$

$a_2$ $b_2$

$:$

$a_M$ $b_M$

出力

問題文の条件を満たすパスが何通りあるか出力せよ。

3 3
1 2
1 3
2 3

2

与えられるグラフは以下の図で表されます。

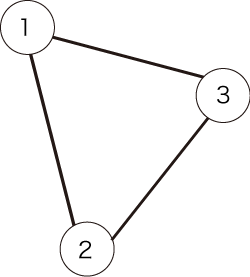
条件を満たすパスは以下の $2$ 通りです。

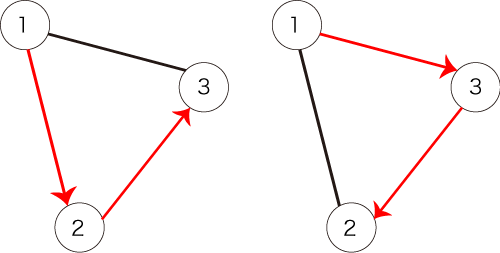
7 7
1 3
2 7
3 4
4 5
4 6
5 6
6 7

1

このテストケースは問題文の例と同じです。