以下是汉化题目。

CF1965C Folding Strip

题目描述

你有一条长度为 $n$ 的纸带，上面写有一个二进制字符串 $s$。你可以在任意一对相邻数字之间对纸带进行折叠。

一组折叠被认为是合法的，当且仅当所有被折叠在一起的字符都相同。注意，所有折叠是同时进行的，因此在折叠之间的字符不需要匹配。

例如，下面是 $s = \mathtt{110110110011}$ 和 $s = \mathtt{01110}$ 的一些合法折叠方式：

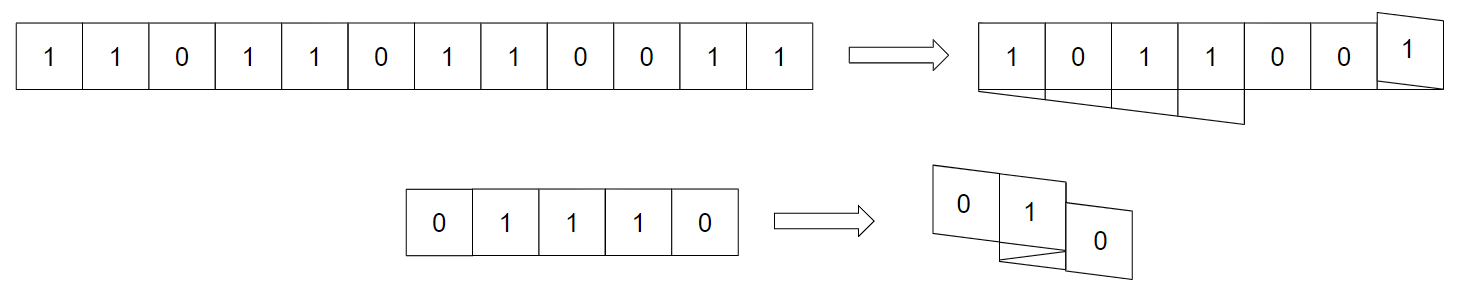
折叠后的纸带长度是所有折叠完成后，从上方看到的纸带长度。因此，对于上面两个例子，折叠后纸带的长度分别为 $7$ 和 $3$。

注意，对于 $s = \mathtt{01110}$ 的上述折叠方式，如果只进行其中任意一个折叠，这都不是合法的折叠方式。然而，因为只有在所有折叠都完成后才检查合法性，所以这种折叠是合法的。

在进行一组合法折叠后，你能得到的纸带的最小长度是多少？

输入格式

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。接下来是每个测试用例的描述。

每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 2\cdot 10^5$），表示纸带的长度。

每个测试用例的第二行包含一个由 $n$ 个字符 '0' 和 '1' 组成的字符串 $s$，表示纸带上的数字。

保证所有测试用例中 $n$ 的总和不超过 $2\cdot 10^5$。

输出格式

对于每个测试用例，输出一个整数，表示经过一组合法折叠后纸带可能的最小长度。

输入输出样例 #1

输入 #1

6
6
101101
1
0
12
110110110011
5
01110
4
1111
2
01

输出 #1

3
1
3
3
1
2

说明/提示

对于第一个示例，最优的折叠方式是将纸带从中间折叠，得到长度为 $3$ 的纸带。

第三个和第四个示例对应上方的图片。注意，对于 $s = \mathtt{110110110011}$ 的折叠方式并不是最小长度的折叠方式。

由 ChatGPT 4.1 翻译