虽然数据范围不大，以为是搜索，但其实是受了“宇宙射线”影响的超级变形背包。可能连一点背包的影子都不见了。

考虑 DP。设状态 $f(i,j,k)$ 表示前 $i$ 个人中选 $j$ 个人，得分差为 $k-400$，最大的得分总和。注意这里得分差不是绝对值差，为了防止下标出现负数，差需要加上 $base=400$。

这道题难于找出答案的具体方案。在 DP 过程中，把所有不合法解全部标为负无穷，从 $base$ 处剖开，不难发现，最终状态中找到的第一个合法状态，就是我们想要的。后面的倒退不难，注意输出格式。

为什么这样就解决问题了呢？要求差最小，把 $base$ 看作 $0$，也就是对于 $v,-v$，如果状态 $f(n,m,v+base)$ 合法，$v$ 的绝对值一定是最小的。至于和最大，DP 迭代过程中已经计算出来了。

// 陪审团
#include <iostream>
#include <cstring>
#include <vector>
#include <cstdio>
#include <algorithm>
#define SIZE 205
#define all(x) x.begin(), x.end()
#define debug(x) cout<<#x<<":"<<x<<endl;
using namespace std;

int n, m; 
int p[SIZE], d[SIZE];
int base=400;
int f[SIZE][21][1000];

signed main()
{
	int COUNT=1;
	while(cin>>n>>m && n+m)
	{
		for(int i=1; i<=n; i++) cin>>p[i]>>d[i];
		memset(f, -0x3f, sizeof(f));
		f[0][0][base]=0;
		for(int i=1; i<=n; i++)
			for(int j=0; j<=m; j++) 
				for(int k=0; k<1000; k++)
				{
					int tmp=k-(p[i]-d[i]);
					if(tmp<0 || tmp>=1000)
					{
						f[i][j][k]=f[i-1][j][k]; continue;
					}
					if(!j)
					{
						f[i][j][k]=f[i-1][j][k]; continue;
					}
					f[i][j][k]=max(f[i-1][j][k], f[i-1][j-1][tmp]+p[i]+d[i]);
				}
		int v=0;
        while(f[n][m][base-v]<0 && f[n][m][base+v]<0) v++;
        if(f[n][m][base-v]>f[n][m][base+v]) v=base-v;
        else v=base+v;
    	
        vector<int> ans;
        int i=n, j=m, k=v;
        while(j)
        {
        	if(f[i][j][k]==f[i-1][j][k]) i--;
        	else
        	{
        		ans.push_back(i); k-=(p[i]-d[i]);
        		i--, j--;
			}
		}
		
		int sp=0, sd=0;
		for(int i=0; i<ans.size(); i++)
			sp+=p[ans[i]], sd+=d[ans[i]];
		printf("Jury #%d\n", COUNT++);
		printf("Best jury has value %d for prosecution and value %d for defence:\n", sp, sd);
		sort(all(ans));
		for(int i=0; i<ans.size(); i++)
			cout<<" "<<ans[i];
		cout<<endl; cout<<endl;
	}

    return 0;
}

注意到题目要求两张卡牌存在至多一项属性值使得两张卡牌该项属性值互质。

这个要求等价于两张卡牌至少有两项属性值的 $\gcd$ 大于 $1$，也就是有至少一个相同的质因数。

我们先暴力枚举这两项属性值是 $AB,AC,BC$ 三种情况。

我们分别枚举 $X$ 中这两个属性值的质因数，以及他们可能形成的组合，将这个质因数组合建出一个点 $id$ 。

然后枚举 $Y$ 中这两个属性值的质因数，以及他们可能形成的组合，查看之前枚举 $X$ 的时候是否有建出对应的点，如果有代表 $X$ 和 $Y$ 这两个属性值存在相同的质因数，也就满足了上面的要求。

那么可以将这个东西进行网络流建模，我们假设左边 $X$ 中第 $i$ 张卡牌包含 $id$ 点所代表的质因数，右边第 $j$ 张卡牌也包含 $id$ 点所包含的质因数。

那么我们可以 $i \rightarrow id$，流量为 $1$，$id \rightarrow (j + n1)$，流量为 $1$。

如此对枚举的两项属性值是 $AB,AC,BC$ 三种情况分别做一遍，然后设置一个源点和汇点与 $X,Y$ 卡牌分别连边，流量为 $1$，之后跑最大流即可。

$200$ 以内的质数只有 $46$ 个，一个数最多 $4$ 个质因子。

我们中间新建出来的点数最多为 $3 \times 46 \times 46$，中间建出来的边数最多为 $16(n1 +n2)$。

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
// 没有力量的理想是戏言，没有理想的力量是空虚
#include <bits/stdc++.h>
#define LL long long
#define int long long
using namespace std;
char ibuf[1 << 15], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, 1 << 15, stdin), p1==p2) ? EOF : *p1++)
inline int read() {
  char ch = getchar();  int x = 0, f = 1;
  while (ch < '0' || ch > '9')  {  if (ch == '-')  f = -1;  ch = getchar();  }
  while (ch >= '0' && ch <= '9')  x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
  return x * f;
}
void print(LL x) {
  if (x > 9)  print(x / 10);
  putchar(x % 10 + '0');
}
template<class T> bool chkmin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool chkmax(T &a, T b) { return a < b ? (a = b, true) : false; }
#define rep(i, l, r) for (int i = (l); i <= (r); i++)
#define repd(i, l, r) for (int i = (l); i >= (r); i--)
#define REP(i, l, r)  for (int i = (l); i < (r); i++)
const int N = 5e6;
int pr[N], cnt, vis[N];
void prime(int n) {
  rep (i, 2, n) {
    if (!vis[i]) {  pr[++cnt] = i;  }
    for (int j = i; j <= n; j += i)  vis[j] = 1;
  }
}
int n1, n2;
map <pair<int,int>, int> id;
int tot, S, T;
int num = 1, nex[N], first[N], v[N], flow[N];
vector <int> ys[205];
int dep[N], cur[N];
queue <int> q;
struct node {  int a, b, c;  } X[N], Y[N];
bool bfs(int s,int t) {
  rep (i, 0, t)  dep[i] = 0;
  q.push(s);  dep[s] = 1;
  while (!q.empty()) {
    int u = q.front();  q.pop();  cur[u] = first[u];
    for (int i = first[u]; i; i = nex[i]) {
      int to = v[i];
      if (dep[to] || !flow[i])  continue;
      q.push(to);  dep[to] = dep[u] + 1;  cur[to] = first[to];
    }
  }
  return dep[t] != 0;
}
int dfs(int x,int a) {
  if (x == T)  return a;
  int ans = 0;
  for (int i = cur[x]; i; i = nex[i]) {
    int to = v[i];
    cur[x] = i; 
    if (dep[to] == dep[x] + 1 && flow[i]) {
      int qwq = dfs(to, min(flow[i], a));
      a -= qwq;  flow[i] -= qwq;  flow[i ^ 1] += qwq;  ans += qwq;
      if (!a)  break;
    }
  }
  return ans;
}
int mxflow(int s,int t) {
  int ans = 0;
  while (bfs(s, t))  ans += dfs(s, 1ll << 30);
  return ans;
}
void add(int from,int to,int val) {
  nex[++num] = first[from];  first[from] = num;  v[num] = to;  flow[num] = val;
}
void ins(int a,int b,int c) {
  add(a, b, c), add(b, a, 0);
}
void solve() {
  prime(200);
  n1 = read(), n2 = read();
  rep (i, 1, n1) {  X[i].a = read(), X[i].b = read(), X[i].c = read();  }
  rep (i, 1, n2) {  Y[i].a = read(), Y[i].b = read(), Y[i].c = read();  }
  tot = n1 + n2;
  sort(pr + 1, pr + cnt + 1);
  rep (x, 1, 200) {
    rep (j, 1, cnt) {
      if (x < pr[j])  continue;
      if (x % pr[j] == 0)  ys[x].push_back(pr[j]);
    }
  }
  // AB
  id.clear();
  rep (i, 1, n1) {
    int A = X[i].a, B = X[i].b;
    for (auto p : ys[A]) {
      for (auto q : ys[B]) {
        int pp = p, qq = q;
        if (id[{pp, qq}] == 0)  {
          id[ {pp, qq} ] = ++tot;
          // cout << 1 << " " << pp << " " << qq << " get id : " << tot << "\n";
        }
        int pt = id[ {pp, qq} ];
        ins(i, pt, 1);
      }
    }
  }
  rep (i, 1, n2) {
    int A = Y[i].a, B = Y[i].b;
    for (auto p : ys[A]) {
      for (auto q : ys[B]) {
        int pp = p, qq = q;
        if (id[ {pp, qq} ] == 0) {
          id[ {pp, qq} ] = ++tot;
        }
        int pt = id[ {pp, qq} ];
        ins(pt, i + n1, 1);
      }
    }
  }
  // AC
  id.clear();
  rep (i, 1, n1) {
    int A = X[i].a, B = X[i].c;
    for (auto p : ys[A]) {
      for (auto q : ys[B]) {
        int pp = p, qq = q;
        if (id[{pp, qq}] == 0) { 
          id[ {pp, qq} ] = ++tot;
        }
        int pt = id[ {pp, qq} ];
        ins(i, pt, 1);
      }
    }
  }
  rep (i, 1, n2) {
    int A = Y[i].a, B = Y[i].c;
    for (auto p : ys[A]) {
      for (auto q : ys[B]) {
        int pp = p, qq = q;
        if (id[ {pp, qq} ] == 0) {
          id[ {pp, qq} ] = ++tot;
        }
        int pt = id[ {pp, qq} ];
        ins(pt, i + n1, 1);
      }
    }
  }
  //BC
  id.clear();
  rep (i, 1, n1) {
    int A = X[i].b, B = X[i].c;
    for (auto p : ys[A]) {
      for (auto q : ys[B]) {
        int pp = p, qq = q;
        if (id[{pp, qq}] == 0)  id[ {pp, qq} ] = ++tot;
        int pt = id[ {pp, qq} ];
        ins(i, pt, 1);
      }
    }
  }
  rep (i, 1, n2) {
    int A = Y[i].b, B = Y[i].c;
    for (auto p : ys[A]) {
      for (auto q : ys[B]) {
        int pp = p, qq = q;
        if (id[ {pp, qq} ] == 0) {
          id[ {pp, qq} ] = ++tot;
        }
        int pt = id[ {pp, qq} ];
        ins(pt, i + n1, 1);
      }
    }
  }
  S = tot + 1, T = tot + 2;
  rep (i, 1, n1)  ins(S, i, 1);
  rep (i, 1, n2)  ins(i + n1, T, 1);
  int ans = mxflow(S, T);
  cout << ans << "\n";
}
signed main () {
#ifdef LOCAL_DEFINE
  freopen("1.in", "r", stdin);
  freopen("1.ans", "w", stdout);
#endif
  int T = 1;  while (T--)  solve();
#ifdef LOCAL_DEFINE
  cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
#endif
  return 0;
}

Solution

考虑对于一个点 $p$，当其同时存在于 $[l_1,~r_1]$ 和 $[l_2,~r_2]$ 内时，由于 $\min_{i = l_1}^{r_1} a_i \le a_p \le \max_{i = l_1}^{r_1} a_i$，所以 $a_p \in f\big((l_1,~r_1)\big)$，同理 $a_p \in f\big((l_2,~r_2)\big)$。也就是说，当两个区间有交时，他们各进行一次 $f$ 操作后分别得到的两个新区间也同样有交。

对于 $[l_1,~r_1],~[l_2,~r_2]~(l_1 \le l_2 \le r_1 \le r_2)$，显然有 $f\big((l_1,~r_2)\big) = f\big((l_1,~r_1)\big) \bigcup f\big((l_2,~r_2)\big)$。而我们通过上面的结论可知等号右侧的两个区间有交，可以通过对左端点取较小值，右端点取较大值的方法得到他们的并。

这启发我们得到：$f\big((l,~r)\big) = \bigcup_{i = l}^{r - 1} f\big((i,~i + 1)\big)$。若预处理得到 $f\big((i,~i + 1)\big) = (x_i,~y_i)$，则 $f\big((l,~r)\big) = (\min_{i = l}^{r - 1} x_i, \max_{i = l}^{r - 1} y_i)$，可通过两个 ST 表做到 $O(1)$ 得出答案。

考虑当我们需要进行多次 $f$ 操作时需要如何计算，由于 $f^{a + b}\big((l,~r)\big) = f^a\Big(f^b\big((l,~r)\big)\Big)$，不难想到使用倍增的思想，对于每个 $k$ 我们预处理 $f^{2^k}\big((i,~i + 1)\big)$，再使用与上面相同的 ST 表维护方法即可 $O(1)$ 算出 $f^{2^k}\big((l,~r)\big)$。

询问 $(l,~r)$ 最少需操作多少次时，我们只需要从大往小枚举 $k$ 找到最大的 $x$ 满足 $f^x\big((l,~r)\big) \neq (1,~n)$，除去无解情况后答案即为 $x + 1$。

总时间复杂度 $O((n + q) \log n)$。

Code

偷了个懒使用线段树实现。复杂度 $O((n + q) \log^2 n)$，也可通过本题。

View on GitHub

/**
 * @file 1707E.cpp
 * @author Macesuted (i@macesuted.moe)
 * @date 2022-07-17
 *
 * @copyright Copyright (c) 2022
 *
 */

#include <bits/stdc++.h>
using namespace std;

#ifndef LOCAL
#define endl '\n'
#endif

bool mem1;

#define maxn 100005
#define maxlgn 18

typedef pair<int, int> pii;

pii merge(const pii& a, const pii& b) { return {min(a.first, b.first), max(a.second, b.second)}; }

class SegmentTree {
   private:
    pii tree[maxn << 2];
    int n;

    void pushUp(int p) { return tree[p] = merge(tree[p << 1], tree[p << 1 | 1]), void(); }
    void insert(int p, int l, int r, int qp, pii v) {
        if (l == r) return tree[p] = v, void();
        int mid = (l + r) >> 1;
        qp <= mid ? insert(p << 1, l, mid, qp, v) : insert(p << 1 | 1, mid + 1, r, qp, v);
        return pushUp(p);
    }
    pii query(int p, int l, int r, int ql, int qr) {
        if (ql <= l && r <= qr) return tree[p];
        int mid = (l + r) >> 1;
        if (qr <= mid) return query(p << 1, l, mid, ql, qr);
        if (ql > mid) return query(p << 1 | 1, mid + 1, r, ql, qr);
        return merge(query(p << 1, l, mid, ql, qr), query(p << 1 | 1, mid + 1, r, ql, qr));
    }

   public:
    void resize(int _n) { return n = _n, void(); }
    void insert(int p, pii v) { return insert(1, 1, n, p, v); }
    pii query(pii a) { return a.first >= a.second ? pii{INT_MAX, INT_MIN} : query(1, 1, n, a.first, a.second - 1); }
};

int a[maxn];
SegmentTree ST[maxlgn];

void solve(void) {
    int n, q;
    cin >> n >> q;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 0; i < maxlgn; i++) ST[i].resize(n);
    for (int i = 1; i < n; i++) ST[0].insert(i, {min(a[i], a[i + 1]), max(a[i], a[i + 1])});
    for (int i = 1; i < maxlgn; i++)
        for (int j = 1; j < n; j++) ST[i].insert(j, ST[i - 1].query(ST[i - 1].query({j, j + 1})));
    while (q--) {
        int l, r;
        cin >> l >> r;
        if (l == 1 && r == n)
            cout << 0 << endl;
        else if (l == r)
            cout << -1 << endl;
        else {
            int ans = 0;
            for (int i = maxlgn - 1; ~i; i--) {
                pii ret = ST[i].query({l, r});
                if (ret != pii{1, n}) ans |= 1 << i, tie(l, r) = ret;
            }
            ans++;
            cout << (ans == (1 << maxlgn) ? -1 : ans) << endl;
        }
    }
    return;
}

bool mem2;

int main() {
    ios::sync_with_stdio(false), cin.tie(nullptr);
#ifdef LOCAL
    cerr << "Memory Cost: " << abs(&mem1 - &mem2) / 1024. / 1024. << "MB" << endl;
#endif

    int _ = 1;
    while (_--) solve();

#ifdef LOCAL
    cerr << "Time Cost: " << clock() * 1000. / CLOCKS_PER_SEC << "MS" << endl;
#endif
    return 0;
}

肯定还是要考虑莫反，但是题目中给定了 $A_i$，这就不能常规的进行反演。

但是其实没有影响的，我们记录每个数 $x$ 的出现次数 $c_x$，然后原式子等价于下面的式子：

于是可以进行反演了。

然后我们套路的改为枚举 $\gcd$。

之后枚举 $x$。

令 $T = xd$，代入进行化简。

对于 $\sum_{d|T} d \times \mu(\dfrac{T}{d}) \times (\dfrac{T}{d})^2$ 这一部分，他等价于 $T \sum_{d|T} \times \mu(\dfrac{T}{d}) \times (\dfrac{T}{d})$，于是我们可以在进行线性筛之后暴力枚举倍数预处理就好了，复杂度是对的。

所以我们只用考虑后面一部分怎么做，也就是 $\sum_{i=1}^{\frac{N}{T}} \sum_{j=1}^{\frac{N}{T}} ij \times c_{\frac{idT}{d}} \times c_{\frac{jdT}{d}}$。

我们发现这东西其实不用写成 $ij$ 两层循环，完全可以写成 $(\sum_{i=1}^{\frac{N}{T}} i \times c_{\frac{idT}{d}})^2 = (\sum_{i=1}^{\frac{N}{T}} i \times c_{iT})^2$。

和上面一样的，莫反题到最后优化也就是整除分块和预处理了。

我们对每个 $T$ 暴力预处理 $\sum_{i=1}^{\frac{N}{T}} i \times c_{iT}$，根据经典结论 $\sum_{i=1}^N \dfrac{N}{i} = n \ln n$。

然后枚举倍数的复杂度也是这样的，所以之前的预处理复杂度也是 $n\ln n$ 的。

于是总预处理复杂度为 $n \ln n$。

最后我们直接暴力回答答案就好了，统计答案的复杂度为 $O(n)$。

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
// 没有力量的理想是戏言，没有理想的力量是空虚
#include <bits/stdc++.h>
#define LL long long
#define int long long
using namespace std;
char ibuf[1 << 15], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, 1 << 15, stdin), p1==p2) ? EOF : *p1++)
inline int read() {
  char ch = getchar();  int x = 0, f = 1;
  while (ch < '0' || ch > '9')  {  if (ch == '-')  f = -1;  ch = getchar();  }
  while (ch >= '0' && ch <= '9')  x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
  return x * f;
}
void print(LL x) {
  if (x > 9)  print(x / 10);
  putchar(x % 10 + '0');
}
template<class T> bool chkmin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool chkmax(T &a, T b) { return a < b ? (a = b, true) : false; }
#define rep(i, l, r) for (int i = (l); i <= (r); i++)
#define repd(i, l, r) for (int i = (l); i >= (r); i--)
#define REP(i, l, r)  for (int i = (l); i < (r); i++)
const int N = 5e4 + 6, M = 5e4 + 5;
int n, vis[N], c[N], pr[N], tot, mu[N];
void prime(int n) {
  mu[1] = 1;
  rep (i, 2, n) {
    if (!vis[i]) {  pr[++tot] = i;  mu[i] = -1;  }
    rep (j, 1, tot) {
      if (pr[j] * i > n)  break;
      vis[i * pr[j]] = 1;
      if (i % pr[j] == 0) {
        mu[i * pr[j]] = 0;  break;
      }  else {
        mu[i * pr[j]] = -mu[i];
      }
    }
  }
}
int f[N], g[N];
void solve() {
  n = read();
  rep (i, 1, n) {  int x = read();  c[x] ++;  }
  prime(M);
  rep (i, 1, M) 
    for (int j = i; j <= M; j += i)  f[j] += mu[i] * i;
  rep (i, 1, M)  f[i] *= i;
  rep (T, 1, M)
    for (int i = 1; i <= M / T; i++)  g[T] += i * c[i * T];
  int ans = 0;
  rep (T, 1, M)  ans += f[T] * g[T] * g[T];
  cout << ans;
}
signed main () {
#ifdef LOCAL_DEFINE
  freopen("1.in", "r", stdin);
  freopen("1.ans", "w", stdout);
#endif
  int T = 1;  while (T--)  solve();
#ifdef LOCAL_DEFINE
  cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
#endif
  return 0;
}

不难发现最后每一行剩下的一定都会是一个连续的区间，而且每行之间相互独立。

自然设立状态 $dp_{i,l,r}$ 表示当前是第 $i$ 行，$k$ 天后这一行剩下的区间为 $[l, r]$，第 $0$ 行到第 $i$ 行都联通的概率。

先考虑算变成区间 $[l,r]$ 的概率。

设 $k$ 天内，消失 $i$ 个格子的概率为 $g_i = \binom{k}{i} p^i \times (1-p)^{k-i}$。

所以剩下区间 $[l,r]$ 的概率为 $g_{l-1} \times g_{m-r}$。

当然还需要检查这段区间长度是否合法，因为最多消失 $2k$ 个格子。

转移式子不难写出。

复杂度 $nm^4$，显然不行，而且状态数都为 $nm^2$。

那考虑优化状态，去掉左端点的限制。

设 $dp_{i,r}$ 表示第 $i$ 行的剩余区间的右端点为 $r$，第 $0$ 行到第 $i$ 行都联通的概率，转移的时候枚举 $l$ 进行转移。

考虑一个和区间 $[l,r]$ 有交的区间 $[l_1,r_1]$。

它满足 $r_1 \geq l, l_1 \leq r$，那么容斥把这一部分算出来即可。

对于 $r_1 < l$ 的部分，枚举 $l$ 时计算 $\sum_{j=1}^{l-1} dp_{i-1,j}$。

对于 $l_1 > r$ 的部分，因为网格是对称的，所以 $f_{i,r}$ 也可以表示左端点为 $m-r+1$ 且联通的概率，因此这一部分可以计算为 $\sum_{j=1}^{m-r} f_{i-1,j}$。

于是转移如下。

这东西长得就很一脸前缀和的样子，那就考虑前缀和优化。

令 $s_{j}$ 表示 $\sum_{k=1}^j f_{i-1,k}$。

在令 $p_i$ 和 $q_i$ 依次为 $g_i$ 与 $g_i \times s_i$ 的前缀和，之后即可做到 $O(1)$ 转移，总时间复杂度 $o(nm)$。

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
#include <bits/stdc++.h>
#define int long long
using namespace std;
inline int read() {
  int x = 0, f = 1;  char ch = getchar();
  while( !isdigit(ch) ) { if(ch == '-') f = -1;  ch = getchar();  }
  while( isdigit(ch) ) {  x = (x << 1) + (x << 3) + (ch ^ 48);  ch = getchar();  }
  return x * f;
}
const int N = 3e6, mod = 1e9 + 7;
int n, m, a, b, pt, pt2, k, ans, fac[N], ifac[N], dp[3005][3005], g[3005];
int power(int a,int b) { int ans = 1; while (b) { if (b & 1) ans = ans * a % mod; a = a * a % mod; b >>= 1;} return ans; }
int binom(int n,int m) { return fac[n] * ifac[m] % mod * ifac[n - m] % mod; }
int s[N], p[N], q[N];
signed main () {
  n = read(), m = read(), a = read(), b = read(), k = read(); 
  fac[0] = 1; for (int i = 1; i <= k; i++) fac[i] = fac[i - 1] * i % mod;
  ifac[k] = power(fac[k], mod - 2); for (int i = k - 1; ~i; i--) ifac[i] = ifac[i + 1] * (i + 1) % mod;
  pt = a * power(b, mod - 2) % mod; pt2 = 1 - pt; pt2 += mod; pt2 %= mod;
  for (int i = 0; i <= k && i <= m; i++) g[i] = binom(k, i) * power(pt, i) % mod * power(pt2, k - i) % mod;
  dp[0][m] = 1;  p[0] = g[0]; 
  for (int i = 1; i <= m; i++) p[i] = p[i - 1] + g[i], p[i] %= mod;
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) s[j] = s[j - 1] + dp[i - 1][j], s[j] %= mod;
    for (int j = 1; j <= m; j++) q[j] = q[j - 1] + g[j] * s[j] % mod, q[j] %= mod;
    for (int r = 1; r <= m; r++) dp[i][r] = g[m - r] * ( (s[m] - s[m - r] + mod) % mod * p[r - 1] % mod - q[r - 1] + mod) % mod;
  }  
  for (int i = 1; i <= m; i++) { ans += dp[n][i]; ans %= mod;}
  printf("%lld\n", ans);
  return 0;
}

为了方便, 以下我们将不加申明的将 $ret$ 用作上一次 $\texttt{query}$ 操作的返回值, 读者可以根据上下文知道这个 $ret$ 的值.

Method 1

我们考虑朴素暴力: 对所有 $i\in [1, n-1]$ 执行操作 $\texttt{query}(\{0, i\})$, 这是一个时间复杂度 $O(n)$ 的算法, 可以获得 ... 10 分.

Method 2

我们发现: 如果已知有 $k$ 个 0, 分别是 $a_{f_1}, a_{f_2}, \cdots a_{f_k}$, 那么可以执行这样的一次操作来求出长度为 $k$ 的序列 $g_1, g_2, \cdots g_k$ 中 0 的个数: $\texttt{query}(\{g_1, f_1, g_2, f_2, \cdots g_k, f_k\})$. 容易知道 $\sum\limits_{i=1}^k g_i = \lceil\frac{ret}{2}\rceil$. 有 $k$ 个 1 的情况下同理.

而如何求出 $f_1, f_2, \cdots f_k$ 呢? 显然直接套用 Method 1 即可. 我们使用类似根号分治的思想可以做到 $O(\sqrt n)$ 的复杂度(实际上后续都是常数优化, 并没有超越这个复杂度.)

Optimize 1

我们考察这种操作: $\texttt{query}(\{g_1, f_1, g_2, f_2, \cdots g_k, f_k\})$. 那么可以根据 $ret$ 的奇偶性判断 $g_1$ 的值, 具体来说, 由于 $g_2, g_3, \cdots g_{k}$ 左右均为相同的值, 故不管这些数如何取值, 均不会影响 $ret$ 的奇偶性, 所以 $ret$ 的奇偶性只由 $a_{g_1}, a_{f_1}$ 决定, 也即可以得出 $a_{g_1}$ 的具体值. 于是我们可以动态的维护当前 0/1 的个数和这些 0/1 的位置然后每次启发式的用 0/1 去询问.

以上优化的代码

Optimize 2

这同时也可以对 Method 1 的过程做出优化: 在有两个相同值的数 $a_x, a_y$ 时, 每次可以通过 $\texttt{query\{p, x, q, y\}}$ 确定 $a_p$, $a_q$ 的具体值.

Optimize 3

Method 2 的过程已经难以优化, 接下来我们来优化 Method 1 的过程.

不妨考虑我们有充分多的 0 和充分多的 1, 接下来我们考虑如何更优的询问, 具体来说, 我们将用 2 询问次得到 5 个数的具体值.

我们设 $p_i$ 为所有 0 的位置序列, $q_i$ 为所有 1 的位置序列. 即 必有 $a_{p_i}=0, a_{q_i}=1$.

我们先进行询问 $\texttt{query}(\{x, p_1, y, p_2, z, p_3\})$. 根据返回值讨论: 首先可以发现根据 $ret$ 的奇偶性确定 $a_x$, 然后我们令 $ret\leftarrow \lfloor\frac{ret}{2}\rfloor$, 这样就有 $a_{y}+a_{z} = ret$. 显然只需要考虑 $ret = 1$ 的情况.

如果 $ret = 1$, 我们接下来进行询问 $\texttt{query}(\{q_1, y, q_2, p_1, z, p_2, u, p_3, v\})$, 然后令 $ret\leftarrow ret-1$(这是因为有相邻的 $q_2, p_1$).

首先考察 $ret$ 的奇偶性以确定 $v$, 然后令 $ret\leftarrow \lfloor \frac{ret}{2}\rfloor$, 这样就有 $1-a_y+a_z+a_u = ret$, 也即 $2a_z+a_u = ret$, 这样又可以根据 $ret$ 的奇偶性来确定 $a_u$, 从而确定 $a_z$ 和 $a_y$.

以上优化的代码

Optimize 4

调整你的参数.

AC 代码

显然，对于一个不是重心的节点，删掉这个点后的连通块里面，最大的连通块就是包含重心的连通块。因此如果叶子添加在重心头上，别的点权值都要加一，重心不变。（对于两个重心的情况，在一个重心上加点时，显然另一个重心权值是要加一的。）

考虑如果不加在重心上。注意到上面提到的性质，哪些节点的权值会改变（如图 1，3 号节点是重心，把它当作根）：

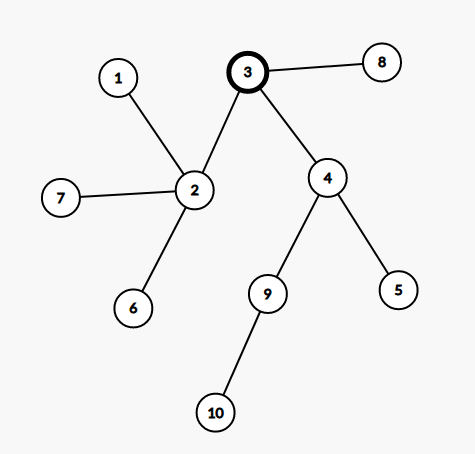
假设我们向 9 号节点添加一个叶子，来分类讨论。

1. 和被添加叶子的点不在同一子树（如 1,2,6,7 号点），显然权值都会加一。
2. 和被添加叶子点在同一侧，不在这个点到根的路径上（如 5,10 号点），考虑到删掉后其最大连通块是根的那一侧，因此权值也会加一。
3. 重心（如 3 号点），若被添加叶子点在重心的最大子树内，则重心权值加一；否则不变。
4. 被添加叶子节点本身（如 9 号点），显然不变。
5. 重心和被添加叶子点路径上的点（如 4 号点），因为删掉它后新叶子没有连通到根，所以不变。

总结一下，如果新叶子在重心的最大子树内，不会改变的就是重心到它的链（不包括两端）；否则，不会改变的是重心到它的链（包括重心，不包括被添加节点）。

我们要维护的是所有点贡献的集合，考虑从重心出发深搜整颗树，到达一个点时，只需要修改这一个点的贡献即可。可以用 Hash 实现。

注意到集合是无序的，如果和我考场降智 naive 地用每个点权值的 $k$ 次方和（$k$ 为常量）当 Hash 函数，注意到 $a^k + b^k = c^k$ 在 $k\leq\log\max(a,b,c)$ 时分布不少，很大概率被卡掉。因此考虑维护每个点权值构成的桶，对这个桶进行字符串 Hash 即可。

单 Hash 也被卡了（我运气背还是出题人毒瘤还是生日悖论再现都有可能），建议双 Hash。

剩下的都是一些细节问题，例如两个重心的情况，可以考虑断掉中间的边，拆成两棵树考虑（在一棵树上时反正另一棵树点的贡献都是要加一的），等等。

#include<bits/stdc++.h>
#define int long long
using namespace std;
bool Begin;
const int max_n=2000006,mod1=1000000009,mod2=998244853;
inline int read(){
    int x=0;bool w=0;char c=getchar();
    while(c<'0' || c>'9') w|=c=='-',c=getchar();
    while(c>='0' && c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return w?-x:x;
}
inline void write(int x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10^48);
}
struct graph{
    int ct,hd[max_n],to[max_n<<1],nx[max_n<<1];
    graph(){ct=1;}
    inline void add(int u,int v){
        nx[++ct]=hd[u],hd[u]=ct,to[ct]=v;
    }
}e;
inline int MOD1(int x){
    return (x>=mod1?x-mod1:x);
}
inline int MOD2(int x){
    return (x>=mod2?x-mod2:x);
}
struct Hashnum{
    int x1,x2;
    Hashnum(int A=0,int B=0):x1(A),x2(B){}
    bool operator == (const Hashnum &b) const{
        Hashnum a=*this;
        return (a.x1==b.x1 && a.x2==b.x2);
    }
    bool operator < (const Hashnum &b) const{
        Hashnum a=*this;
        return (a.x1<b.x1 || (a.x1==b.x1 && a.x2<b.x2));
    }
    Hashnum operator * (const Hashnum &b) const{
        Hashnum a=*this;
        return Hashnum(a.x1*b.x1%mod1,a.x2*b.x2%mod2);
    }
    Hashnum operator + (const Hashnum &b) const{
        Hashnum a=*this;
        return Hashnum(MOD1(a.x1+b.x1),MOD2(a.x2+b.x2));
    }
    Hashnum operator - (const Hashnum &b) const{
        Hashnum a=*this;
        return Hashnum(MOD1(a.x1-b.x1+mod1),MOD2(a.x2-b.x2+mod2));
    }
    Hashnum operator * (const int &b) const{
        Hashnum a=*this;
        return a*Hashnum(b,b);
    }
    Hashnum operator + (const int &b) const{
        Hashnum a=*this;
        return a+Hashnum(b,b);
    }
    Hashnum operator - (const int &b) const{
        Hashnum a=*this;
        return a-Hashnum(b,b);
    }
}hs;

int n,sz[max_n],mxs[max_n];

inline void dfs1(int u,int fa){
    sz[u]=1;
    for(register int i=e.hd[u];i;i=e.nx[i]){
        int v=e.to[i];
        if(v==fa) continue;
        dfs1(v,u);
        sz[u]+=sz[v];
        mxs[u]=max(mxs[u],sz[v]);
    }
    mxs[u]=max(mxs[u],n-sz[u]);
}
int zx,zx2;
inline void dfs2(int u,int fa){
    zx=u;
    for(register int i=e.hd[u];i;i=e.nx[i]){
        int v=e.to[i];
        if(v==fa) continue;
        if(sz[v]>n/2)
            dfs2(v,u);
    }
}

int ans[max_n],tong[max_n],pw1[max_n],pw2[max_n];

int B1=114514,B2=11037;

map<Hashnum,int> mp;
inline void dfs3(int u,int fa,Hashnum hs){
    for(register int i=e.hd[u];i;i=e.nx[i]){
        int v=e.to[i];
        if(v==fa || v==zx || v==zx2) continue;
        Hashnum t=hs-Hashnum(pw1[mxs[v]+1],pw2[mxs[v]+1])+Hashnum(pw1[mxs[v]],pw2[mxs[v]]);
        ++mp[t];
        dfs3(v,u,t);
    }
}

bool End;
#define File "forest"
signed main(){
    // #ifndef ONLINE_JUDGE
    // freopen(File ".in","r",stdin);
    // freopen(File ".out","w",stdout);
    // #endif
    // cerr<<"Memory : "<<(&Begin-&End)/1024.0/1024<<"\n";
    n=read();
    for(register int i=1;i<n;++i){
        int u=read(),v=read();
        e.add(u,v),e.add(v,u);
    }
    dfs1(1,-1);
    dfs2(1,-1);
    for(register int i=1;i<=n;++i)
        ++tong[mxs[i]+1];
    ++tong[n];
    if(!(n&1)) for(register int i=1;i<=n;++i)
        if(i!=zx && mxs[i]==mxs[zx]){
            zx2=i;
            break;
        }
    for(register int i=1;i<=n;++i){
        hs.x1=(hs.x1*B1+tong[i]),
        hs.x2=(hs.x2*B2+tong[i]);
    }
    pw1[n]=pw2[n]=1;
    for(register int i=n-1;i;--i){
        pw1[i]=pw1[i+1]*B1%mod1,
        pw2[i]=pw2[i+1]*B2%mod2;
    }
    ++mp[hs-Hashnum(pw1[mxs[zx]+1],pw2[mxs[zx]+1])+Hashnum(pw1[mxs[zx]],pw2[mxs[zx]])];
    if(zx2) ++mp[hs-Hashnum(pw1[mxs[zx2]+1],pw2[mxs[zx2]+1])+Hashnum(pw1[mxs[zx2]],pw2[mxs[zx2]])];
    dfs3(zx,-1,hs);
    if(zx2) dfs3(zx2,-1,hs);
    int cnt=0;
    for(auto i=mp.begin();i!=mp.end();++i)
        ans[++cnt]=(*i).second;
    sort(ans+1,ans+1+cnt);
    write(cnt),putchar('\n');
    for(register int i=1;i<=cnt;++i)
        write(ans[i]),putchar('\n');
    return 0;
}

Solution

第一问建图后直接最大流即可得出。

酿酒代价为二次函数不易于计算，一个自然的想法是将这个二次函数从定义域上切割为若干段，将每一段内的部分近似为一个一次函数，然后就可以对于每一段建立一条对应的边，跑费用流即可。由于此处二次函数斜率递增，定义域靠前的段在代价上优于靠后的段，因此不需要考虑取这些段的先后顺序而可能带来的不合法取法。

但是此题要求输出分数，也就是不允许误差的存在。我们发现上面的做法分的段数越多，结果误差就越小，当每一段的长度无线接近于零，段数接近正无穷时误差即可消除。此时每一段内的一次函数就成为了该二次函数的导数：$2 a_i x + b_i$。

虽然解决了误差问题，但是段数达到了正无穷，我们无法直接对于每一段建边跑费用流。但是我们发现，若假设存酒点容量无穷，即只考虑产酒点总产量而不考虑存酒点限制的情况下，所有的最优方案一定是这样的：存在一个实数 $l$ 作为阈值，每一个产酒点对应的花费二次函数上导数小于 $l$ 的部分对应的定义域大小即为该产酒点产量。贪心策略下显然成立。

因此我们考虑构建函数 $F(x)$ 表示当阈值为 $x$ 时，不考虑存酒点限制情况下的产酒点总产量。若令 $F_i(x)$ 表示阈值为 $x$ 时第 $i$ 个产酒点的产量，可以发现 $F_i(x) = \frac 1 {2a_i} x - \frac {b_i} {2a_i} (x \in [b_i,~2 a_i c_i + b_i])$。而 $F(x) = \sum_i F_i(x)$，所以 $F(x)$ 应当由 $O(n)$ 个一次函数首尾相连形成。

该阈值与费用流 SPFA 跑出的 $dist[T]$ 功能类似，若要模拟费用流过程，我们可以令阈值从 $0$ 开始不断增长，每次更改阈值后重新通过 $F_i(x)$ 计算每条边的对应流量。费用流过程中还可将存酒点的流量限制加入，从而算出考虑存酒点限制情况下的总产量。

由于不允许存在精度误差因此我们无法做到真正模拟该过程，但是通过这个思路我们发现在阈值不断增加的过程中，存酒点总是先尽可能多地存酒，直至其容量达到上限后对部分酿酒点的产量产生限制。也就是说，我们可以通过 $F(x)$ 结合网络流得到 $G(x)$ 表示考虑存酒点容量限制的情况下，阈值为 $x$ 时的总产量。$G(x)$ 只会在 $F(x)$ 的基础上多 $O(m)$ 个端点，其图像由 $O(n + m)$ 个一次函数首尾相连形成。

但是 $G(x)$ 不像 $F(x)$ 可以直接通过计算得出，$G(x)$ 的每一个点都需要网络流计算得出。不过我们发现 $G(x)$ 的大部分图像呈现上凸壳的形态，我们可以在定义域上分治得到整个图像：令 $solve(l,~r)$ 过程查找横坐标在 $(l,~r)$ 间的所有端点位置，我们在 $l$ 和 $r$ 上分别用网络流算出坐标，并结合残量网络算出斜率，可得两个端点处的一次函数。取这两个一次函数的交点，令其为 $mid$，计算 $mid$ 处的一次函数，若与两端的一次函数相同则说明 $(l,~r)$ 范围内已再无端点，否则向 $(l,~mid)$ 和 $(mid,~r)$ 递归求解。但是注意到 $a_i$ 可能等于零，也就是说一些一次函数可能出现斜率无穷的情况，因此需要在 $x = 0,~1,~2,~3$ 处强制断开，在 $(0,~1),~(1,~2),~(2,~3),~(3,~+\infty)$ 段分开分治求解。

计算出 $G(x)$ 的图像后，通过计算其积分即可得到最终答案。

Code

View on GitHub

/**
 * @file 2138.cpp
 * @author Macesuted (i@macesuted.moe)
 * @date 2022-07-05
 *
 * @copyright Copyright (c) 2022
 *
 */

#include <bits/stdc++.h>
using namespace std;

#ifndef LOCAL
#define endl '\n'
#endif

bool mem1;

#define maxn 105
#define eps 1e-9
#define feps 1e-11

bool con[maxn][maxn];
int n, m, a[maxn], b[maxn], c[maxn], d[maxn];

class Frac {
   private:
    int64_t x, y;

    int64_t gcd(int64_t a, int64_t b) { return b ? gcd(b, a % b) : a; }

   public:
    Frac(int64_t x_ = 0, int64_t y_ = 1) {
        int64_t g = gcd(x_, y_);
        x = x_ / g, y = y_ / g;
    }
    operator double() { return (double)x / y; }
    operator int64_t() { return x / y; }
    Frac operator+(const Frac& o) const { return Frac(x * o.y + y * o.x, y * o.y); }
    Frac operator-(const Frac& o) const { return Frac(x * o.y - y * o.x, y * o.y); }
    Frac operator*(const Frac& o) const { return Frac(x * o.x, y * o.y); }
    Frac operator/(const Frac& o) const { return Frac(x * o.y, y * o.x); }
    bool operator==(const Frac& o) const { return x == o.x && y == o.y; }
    Frac& operator+=(const Frac& o) { return *this = *this + o; }
    Frac& operator-=(const Frac& o) { return *this = *this - o; }
    Frac& operator*=(const Frac& o) { return *this = *this * o; }
    Frac& operator/=(const Frac& o) { return *this = *this / o; }
    void print(void) {
        if (y < 0) x = -x, y = -x;
        return cout << x << '/' << y, void();
    }
};

typedef pair<Frac, Frac> pff;

class Dinic {
   private:
    struct Edge {
        int to, rev;
        double cap;
    };

    vector<vector<Edge>> graph;
    vector<vector<Edge>::iterator> cur;
    vector<int> dist;
    queue<int> que;

    bool bfs(void) {
        for (int i = 1; i <= n + m + 2; i++) dist[i] = -1, cur[i] = graph[i].begin();
        que.push(n + m + 1), dist[n + m + 1] = 0;
        while (!que.empty()) {
            int p = que.front();
            que.pop();
            for (auto i : graph[p])
                if (i.cap > feps && !~dist[i.to]) dist[i.to] = dist[p] + 1, que.push(i.to);
        }
        return ~dist[n + m + 2];
    }
    double dfs(int p, double rest) {
        if (rest < feps || p == n + m + 2) return rest;
        double use = 0, c;
        for (auto i = cur[p]; i != graph[p].end() && rest > feps; i++) {
            cur[p] = i;
            if (dist[p] + 1 != dist[i->to] || i->cap < feps) continue;
            if ((c = dfs(i->to, min(rest, i->cap))) < feps) dist[i->to] = -1;
            i->cap -= c, graph[i->to][i->rev].cap += c, use += c, rest -= c;
        }
        return use;
    }

   public:
    void addEdge(int from, int to, double cap) {
        return graph[from].push_back(Edge{to, (int)graph[to].size(), cap}),
               graph[to].push_back(Edge{from, (int)graph[from].size() - 1, 0});
    }
    pff dinic(double lim) {
        graph.clear(), graph.resize(n + m + 3), cur.resize(n + m + 3), dist.resize(n + m + 3);
        for (int i = 1; i <= n; i++)
            if (a[i] == 0) {
                if (b[i] < lim) addEdge(n + m + 1, i, c[i]);
            } else
                addEdge(n + m + 1, i, min((lim - b[i]) / 2. / a[i], (double)c[i]));
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                if (con[i][j]) addEdge(i, n + j, 1e18);
        for (int i = 1; i <= m; i++) addEdge(n + i, n + m + 2, d[i]);
        while (bfs()) dfs(n + m + 1, 1e18);
        Frac K, B;
        for (int i = 1; i <= n; i++)
            if (dist[i] == -1) {
                if (a[i] == 0) {
                    if (b[i] < lim) B += Frac(c[i]);
                } else if (lim > 2 * a[i] * c[i] + b[i])
                    B += Frac(c[i]);
                else if (lim > b[i])
                    K += Frac(1, 2 * a[i]), B -= Frac(b[i], a[i] * 2);
            }
        for (int i = 1; i <= m; i++)
            if (~dist[n + i]) B += Frac(d[i]);
        return {K, B};
    }
} net;

vector<pff> nodes;

void solve(pff l, pff r) {
    if (l == r) return;
    Frac mid = (l.second - r.second) / (r.first - l.first);
    pff fml = net.dinic((double)mid - eps), fmr = net.dinic((double)mid + eps);
    if (l == fml) return nodes.emplace_back(mid, fml.first * mid + fml.second), void();
    return solve(l, fml), solve(fmr, r);
}

void solve(void) {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> a[i] >> b[i] >> c[i];
    for (int i = 1; i <= m; i++) cin >> d[i];
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) cin >> con[i][j];
    cout << int64_t(net.dinic(1e18).second) << endl;
    nodes.emplace_back(Frac(), Frac());
    for (int i = 1; i <= 3; i++) {
        auto l = net.dinic(i - 1 + eps), r = net.dinic(i - eps);
        solve(l, r);
        nodes.emplace_back(Frac(i), Frac(i) * r.first + r.second);
    }
    solve(net.dinic(3 + eps), net.dinic(1e18));
    Frac ans;
    for (int i = 1; i < (int)nodes.size(); i++) {
        pff f1 = net.dinic((double)nodes[i - 1].first + eps), f2 = net.dinic((double)nodes[i].first - eps),
            f3 = net.dinic((double)nodes[i].first + eps);
        ans += Frac(1, 2) * (nodes[i].second - f1.first * nodes[i - 1].first - f1.second) *
                   (nodes[i - 1].first + nodes[i].first) +
               nodes[i].first * (f3.first * nodes[i].first + f3.second - f2.first * nodes[i].first - f2.second);
    }
    ans.print(), cout << endl;
    return;
}

bool mem2;

int main() {
    ios::sync_with_stdio(false), cin.tie(nullptr);
#ifdef LOCAL
    cerr << "Memory Cost: " << abs(&mem1 - &mem2) / 1024. / 1024. << "MB" << endl;
#endif

    int _ = 1;
    while (_--) solve();

#ifdef LOCAL
    cerr << "Time Cost: " << clock() * 1000. / CLOCKS_PER_SEC << "MS" << endl;
#endif
    return 0;
}

如果四个边界上没有格子被染色，是一个经典套路，考虑构造“梳子”状的图案，如图 1：

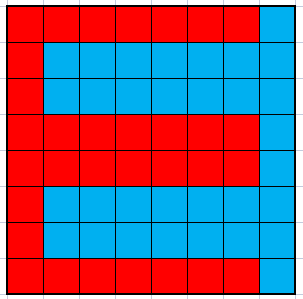
因为任意两个限制颜色的格子不八联通，这种方案一定是可行的。

然后考虑如果边界上有限制颜色的格子。若边界上存在形如 BWBW 的序列，是一定无解的，如图 2（格子上有“限制”二字表示这个格子颜色固定）：

对于不存在形如 BWBW 序列的情况，不难发现，我们一定可以找到完整的一个边界（上/下/左/右），这条边上可以全部赋成同一个颜色，而且它对面那条边界上至少有一个点是不同的颜色。不妨把这个完整的边界上的颜色当成蓝色，参考图 1 “梳子”型构造的蓝色部分，给它安排好。以保证蓝色的格子相互之间可以连通了。现在处理红色格子，可以列举出如下三个不合法的情况，我们一一解决：

1. 边框被蓝色包围了，部分边框上的红色与梳子的条纹不联通。
2. 接近边框位置（第 $2$ 和第 $n-1$ 行）的格子不联通。
3. 红色梳子条纹不联通。

图 3 的三个例子分别对应了上面的三种不合法情况：

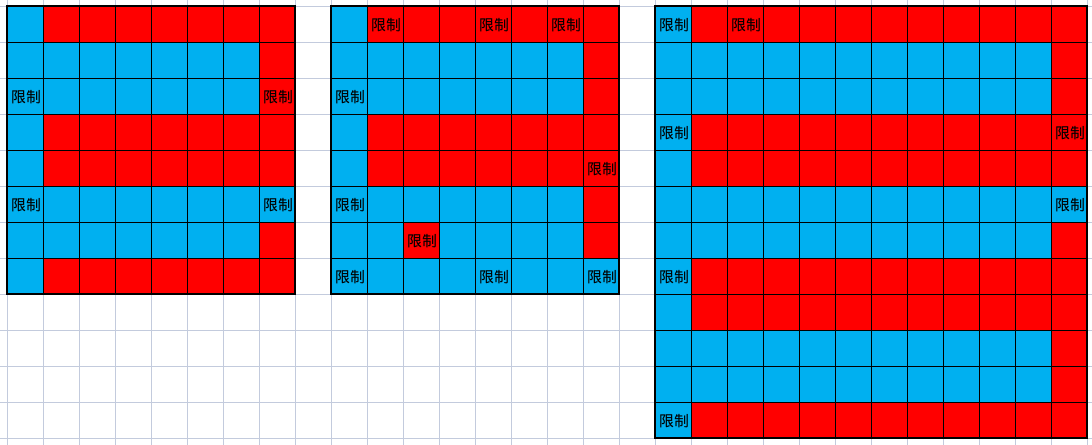
实际上这三种情况都可以通过简单的调整实现：

1. 把下面也变成蓝色。（显然）
2. 直接把道路打通就可以了，因为旁边的蓝色一定是连通的（考虑 BWBW 情况已经没有了，如果不联通就扩充直到顶到一个限制红色的格子门口）。
3. 打穿一个蓝色条纹即可，这一步在实现情况二之后进行，就无需考虑被打穿的蓝色条纹左右不联通了（两边的条纹会沿着一条边界连起来）。

此外还有很多零零散散的细节，例如解决这三种情况的顺序，等等。

#include<bits/stdc++.h>
#define int long long
using namespace std;
bool Begin;
const int max_n=502;
inline int read(){
    int x=0;bool w=0;char c=getchar();
    while(c<'0' || c>'9') w|=c=='-',c=getchar();
    while(c>='0' && c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return w?-x:x;
}
inline void write(int x){
    putchar(x==2?'B':'W');
}
inline int reads(){
    char c=getchar();
    while(c!='B' && c!='W' && c!='.') c=getchar();
    if(c=='B') return 2;
    if(c=='W') return 3;
    return 0;
}

int n,m,cntr;
int a[max_n][max_n],ans[max_n][max_n];

int Tmp[max_n][max_n];
inline void rotate(){
    for(register int i=1;i<=n;++i)
        for(register int j=1;j<=m;++j)
            Tmp[i][j]=a[i][j];
    for(register int i=1;i<=n;++i)
        for(register int j=1;j<=m;++j)
            a[j][n-i+1]=Tmp[i][j];
    for(register int i=1;i<=n;++i)
        for(register int j=1;j<=m;++j)
            Tmp[i][j]=ans[i][j];
    for(register int i=1;i<=n;++i)
        for(register int j=1;j<=m;++j)
            ans[j][n-i+1]=Tmp[i][j];
    swap(n,m),++cntr;
}
inline void clear(){
    cntr=0;
    for(register int i=0;i<=n;++i)
        for(register int j=0;j<=m;++j)
            a[i][j]=ans[i][j]=a[j][i]=ans[j][i]=0;
}

inline int calc(){
    int res=0;
    for(register int p=1;p<=2;++p){
        for(register int i=2;i<=m;++i)
            if(!ans[1][i])
                ans[1][i]=ans[1][i-1];
        for(register int i=2;i<=n;++i)
            if(!ans[i][m])
                ans[i][m]=ans[i-1][m];
        for(register int i=m-1;i;--i)
            if(!ans[n][i])
                ans[n][i]=ans[n][i+1];
        for(register int i=n-1;i;--i)
            if(!ans[i][1])
                ans[i][1]=ans[i+1][1];
        if(!ans[1][1])
            ans[1][1]=2;
    }
    for(register int i=2;i<=m;++i)
        if(ans[1][i]!=ans[1][i-1])
            ++res;
    for(register int i=2;i<=n;++i)
        if(ans[i][m]!=ans[i-1][m])
            ++res;
    for(register int i=m-1;i;--i)
        if(ans[n][i]!=ans[n][i+1])
            ++res;
    for(register int i=n-1;i;--i)
        if(ans[i][1]!=ans[i+1][1])
            ++res;
    return res;
}

inline bool Nice(){
    bool ok=0;
    for(register int i=1;i<=n;++i){
        if(ans[i][1]!=ans[1][1])
            return 0;
        if(i>1 && i<n && ans[i][m]!=ans[1][1])
            ok=1;
    }
    return ok;
}

int Red,Blue;

inline void findroad(int x,int y){
    if(ans[x-1][y]==Red || ans[x+1][y]==Red || ans[x][y+1]==Red) return;
    int X1=(x==2?1:n);
    if(y<=m-2 && ans[X1][y+2]==Red){
        ans[X1][y]=ans[X1][y+1]=Red;
        return;
    }
    int X2=(x==2?2:n-1);
    if(y<=m-2 && ans[X2][y+2]==Red){
        ans[X2][y+1]=Red;
        return;
    }
    int X3=(x==2?3:n-2),X4=(x==2?4:n-3);
    if(a[X4][y]!=Blue){
        ans[X3][y]=Red;
        return;
    }
    int Y=(y<=m-2?y+1:y-1);
    ans[X2][Y]=ans[X3][Y]=Red;
}

inline void bigroad(int x){
    for(register int j=2;j<=4;++j){
        bool ok=1;
        for(register int i=x-1;i<=x+2;++i)
            if(a[i][j]==Blue){
                ok=0;
                break;
            }
        if(ok){
            ans[x][j]=ans[x+1][j]=Red;
            return;
        }
    }
    for(register int i=x-1;i<=x+2;++i)
        if(!a[i][3])
            ans[i][3]=Red;
    if(a[x-1][3]){
        ans[x-1][2]=Blue,
        ans[x][4]=Red;
    }
    if(a[x+2][3]){
        ans[x+2][2]=Blue,
        ans[x+1][4]=Red;
    }
    if(a[x][3] || a[x+1][3]){
        ans[x][2]=ans[x+1][2]=Red;
    }
}

inline void buildroad(){
    int fr=0,ls=0;
    for(register int i=1;i<=n;++i)
        if(ans[i][m]==Red){
            if(!fr) fr=i;
            ls=i;
        }
    if(!fr || (ls>3 && fr<n-2)) return;
    if(ls<=3 && a[4][m-1]==Blue){
        ans[3][m]=ans[4][m]=ans[5][m]=Red;
        return;
    }
    if(fr>=n-2 && a[n-3][m-1]==Blue){
        ans[n-4][m]=ans[n-3][m]=ans[n-2][m]=Red;
        return;
    }
    int x=(ls<=3?2:n-2);
    for(register int i=x;i<=x+1;++i)
        for(register int j=m-1;j<=m;++j)
            if(!a[i][j])
                ans[i][j]=Red;
}

bool End;
#define File ""
signed main(){
    // #ifndef ONLINE_JUDGE
    // freopen(File ".in","r",stdin);
    // freopen(File ".out","w",stdout);
    // #endif
    for(register int T=read();T;--T,clear()){
        n=read(),m=read();
        for(register int i=1;i<=n;++i)
            for(register int j=1;j<=m;++j)
                a[i][j]=ans[i][j]=reads();
        int tmp=calc();
        if(tmp>=4){
            puts("NO");
            continue;
        }
        if(tmp>0) while(!Nice()) rotate();
        Blue=ans[1][1],Red=Blue^1;
        for(register int i=2;i<n;++i)
            for(register int j=2;j<m;++j)
                if(!a[i][j])
                    ans[i][j]=(i%4>1?Blue:Red);
        for(register int i=1;i<n;++i)
            if(ans[i][m-1]==ans[i+1][m] && ans[i+1][m-1]==ans[i][m] && ans[i][m]!=ans[i+1][m]){
                if(!a[i][m]) ans[i][m]^=1;
                else ans[i+1][m]^=1;
            }
        buildroad();
        for(register int i=2;i<m;++i){
            if(a[2][i]==Red) findroad(2,i);
            if(a[n-1][i]==Red) findroad(n-1,i);
        }
        for(register int i=6;i<=n-6;i+=4)
            if(ans[i][m]==Blue || ans[i+1][m]==Blue)
                bigroad(i);
        while(cntr%4!=0) rotate();
        puts("YES");
        for(register int i=1;i<=n;++i){
            for(register int j=1;j<=m;++j)
                write(ans[i][j]);
            putchar('\n');
        }
    }
    return 0;
}

考虑 lyndon 分解，如果我们对每个前缀都跑一遍 lyndon 分解的话，答案应该是最后一个开头 $\leq i$ 的 lyndon 串。

这样不优秀啊，但是我们仍然考虑 lyndon 分解。

假设我们现在维护的是 $pu^tv$，仍然维护指针 $i,j,k$。

我们其实当前位置要加入的一个字符 $k$ 的最小表示法的开头只会有两种情况，一种是在我的当前开始的位置 $i$，一种是在我加入的这个 $v$ 里面的。

在 $v$ 里面的话，你考虑他最终的表示法会是什么样子，比如 $pu^tv$，那么最终他会是 $vpu^t$。

你仔细发现，反正我没发现，然后你发现如果你去掉最后的 $|u|$ 个字符，他就会变成 $vpu^{t-1}$，然后这就是一个已经求解过的答案了，他是 $pu^{t-1}v$ 的最小表示法。

现在我们需要根据 $S_j$ 和 $S_k$ 的大小进行分类。

如果 $S_j < S_k$，那么根据 lyndon 串的性质，那么 $u^tv+S_k$ 仍然是一个 lyndon 串，那么此时的 $i$ 就是我们的 $ans_k$。

如果 $S_j > S_k$，那么之前的 lyndon 串被划分了出来，但是当前位置仍然不知道，于是我们将其放到后面进行求解。

如果 $S_j = S_k$，那么可以选择两种位置，首先就是当前的 $i$ 可以作为 $ans_k$，另一种是，先前循环节中 $k$ 的对应位置 $j$ 的答案向后移一个循环节的对应位置 $ans_j + k - j$。

那么需要比较的为 $S[i\dots k] + S[1 \dots (i - 1)]$ 和 $S[(ans_j + k - j) \dots k] + S[1\dots ans_{j} + k - j - 1]$ 的字典序大小。

首先我们只会在 $S_j = S_k$ 的时候遇到这种情况，那么 $S[i \dots (i + k - (ans_j + k - j))]$ 和 $S[(ans_j + k - j) \dots k]$ 肯定都是相同的。

如下图：

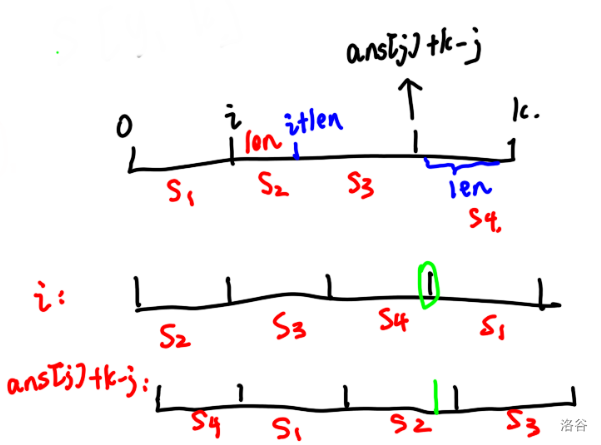
也就是说上面的 $S_2$ 和 $S_4$ 一定是相同的。

然后你分着来比较，先比较 $S_3 + S_4$ 和与他对应长度的那一部分。

也就是图中画着绿线的那一部分，然后再比较后面的剩下部分就好了。

这样你发现，每次都是将一个子串 $S[a \dots b]$ 与原串的一个前缀 $S[1 \dots b - a + 1]$ 进行比较。

那么我们可以使用 $z$ 函数，判断后缀 $a$ 与原串的一个 lcp 长度判断是否再比较范围内，并找到这个不同即可。

使用 $\text{exkmp}$ 可以求解。

于是直接跑 Duval 算法就好了，复杂度 $O(n)$，真神仙。

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
// 没有力量的理想是戏言，没有理想的力量是空虚
// Problem: P5334 [JSOI2019]节日庆典
// Contest: Luogu
// Memory Limit: 500 MB
// Time Limit: 1000 ms
// The Author : Pt
#include <bits/stdc++.h>
using namespace std;
namespace io {
  const int SIZE = (1 << 21) + 1; char ibuf[SIZE], *iS, *iT, obuf[SIZE], *oS = obuf, *oT = oS + SIZE - 1, c, qu[55]; int f, qr;
  #define gc() (iS == iT ? (iT = (iS = ibuf) + fread (ibuf, 1, SIZE, stdin), (iS == iT ? EOF : *iS ++)) : *iS ++)
  inline void flush () {  fwrite (obuf, 1, oS - obuf, stdout); oS = obuf; }
  inline void putc (char x) { *oS ++ = x; if (oS == oT) flush (); }
  template <class I> inline void gi (I &x) { for (f = 1, c = gc(); c < '0' || c > '9'; c = gc()) if (c == '-') f = -1; for (x = 0; c <= '9' && c >= '0'; c = gc()) x = x * 10 + (c & 15); x *= f; }
  string getstr(void) { string s = ""; char c = gc(); while (c == ' ' || c == '\n' || c == '\r' || c == '\t' || c == EOF) c = gc(); while (!(c == ' ' || c == '\n' || c == '\r' || c == '\t' || c == EOF))s.push_back(c), c = gc(); return s;}
  template <class I> inline void print (I x) { if (!x) putc ('0'); if (x < 0) putc ('-'), x = -x; while (x) qu[++ qr] = x % 10 + '0',  x /= 10; while (qr) putc (qu[qr --]); }
  struct Flusher_ {~Flusher_(){flush();}}io_flusher_;
}
using io :: gi;  using io :: putc;  using io :: print;
#define V inline void
#define I inline int
template<class T> bool chkmin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool chkmax(T &a, T b) { return a < b ? (a = b, true) : false; }
#define rep(i, l, r) for (int i = (l); i <= (r); i++)
#define repd(i, l, r) for (int i = (l); i >= (r); i--)
const int N = 3e6 + 5;
char S[N];
int z[N], n, ans[N];
void exkmp() {
  z[1] = n;
  for (int i = 2, l = 0, r = 0; i <= n; i++) {
    if (i <= r)  z[i] = min(z[i - l + 1], r - i + 1);
    while (i + z[i] <= n && S[i + z[i]] == S[1 + z[i]]) ++ z[i];
    if (i + z[i] - 1 > r)  r = i + z[l = i] - 1;
  }
}
int compare(int x,int y,int r) {
  if (x == y)  return x;
  int zz = z[x + r - y + 1];
  if (zz < y - x)  return S[x + r - y + 1 + zz] < S[1 + zz] ? x : y;
  zz = z[y - x + 1];
  if (zz < x - 1)  return S[1 + zz] < S[y - x + 1 + zz] ? x : y;
  return x;
}
void solve() {
  int i = 1;
  while (i <= n) {
    int j = i, k = i + 1;
    if (!ans[i])  ans[i] = i;
    while (k <= n && S[j] <= S[k]) {
      if (S[j] < S[k]) {
        if (!ans[k])  ans[k] = i;  j = i;  ++k;
      }  else {
        if (!ans[k]) {
          if (ans[j] < i)  ans[k] = i;
          else  ans[k] = compare(i, ans[j] + k - j, k);
        }
        ++k;  ++j;
      }
    }
    int len = k - j;
    while (i <= j)  i += len;
  }
}
signed main () {
#ifdef LOCAL_DEFINE
  freopen("input.txt", "r", stdin);
#endif
  cin >> (S + 1);  n = strlen(S + 1);
  exkmp();  solve();
  rep (i, 1, n)  cout << ans[i] << " ";
#ifdef LOCAL_DEFINE
  cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
#endif
  return 0;
}

考虑一个较低的列，它将区间划分为左右两边，高于这个列高的位置在左右两边互不攻击。

找到全局最低的列，递归地跑两边的背包（棋子数，方案数），然后合并左右区间的背包，剩下的部分是在一个与该最低列同高的，宽度为区间长度减去已经选的列的矩形上放置 $k$ 个车，这个东西可以很快地组合数（选 $k$ 行 $k$ 列然后选择一种排列代表棋子的位置）：

将合并得到的背包和当前的决策再做一遍卷积，得到当前区间的背包。

由于 $k$ 比较小，暴力卷就行了。

找区间最小值的过程实际上就是一个小根笛卡尔树，所以 $\mathcal{O}(n)$ 预先建立笛卡尔树然后在树上跑这个背包的过程即可。

注意在递归过程中子区间当前结点的决策高度应该是当前列的高度减去上次划分的高度（笛卡尔树的父节点）。

然后如果刚开始想到用最小值划分区间类似的东西，就可以建出笛卡尔树来辅助思考。

code

const int maxn = 510, maxc = 1e6 + 10, mod = 1e9 + 7;
inline int inc(int x, int y) { return (x += y) < mod ? x : x - mod; }
inline int dec(int x, int y) { return (x -= y) < 0 ? x + mod : x; }
inline int mul(int x, int y) { return 1ll * x * y % mod; }
inline int qp(int x, int y) {
    int ret = 1 % mod;
    for(; y; y >>= 1) {
        if(y & 1) ret = mul(ret, x);
        x = mul(x, x);
    }
    return ret;
}
int a[maxn], ls[maxn], rs[maxn], siz[maxn], root;
int f[maxn][maxn], tmp[maxn];
int fac[maxc], invF[maxc];
int n, k;

inline int C(int x, int y) {
    return mul(fac[x], mul(invF[x - y], invF[y]));
}
inline int calc(int x, int y, int k) {
    if(min(x, y) < k) return 0;
    return mul(mul(C(x, k), C(y, k)), fac[k]);
}
void dfs(int cur, int pre) {
    siz[cur] = 1;
    if(ls[cur]) dfs(ls[cur], cur), siz[cur] += siz[ls[cur]];
    if(rs[cur]) dfs(rs[cur], cur), siz[cur] += siz[rs[cur]];
    memset(tmp,0,sizeof(tmp));
    rep(i,0,min(siz[ls[cur]],k))
        rep(j,0,min(k - i,siz[rs[cur]]))
            tmp[i + j] = inc(tmp[i + j], mul(f[ls[cur]][i], f[rs[cur]][j]));
    rep(i,0,min(siz[cur],k))
        rep(j,0,min(siz[cur] - 1, i))
          f[cur][i] = inc(f[cur][i], mul(tmp[j], calc(siz[cur] - j, a[cur] - a[pre], i - j)));
}

signed main() {
    n = read(); k = read();
    int c = n;
    rep(i,1,n) a[i] = read(), c = max(c, a[i]);
    if(n < k) {
        puts("0");
        return 0;
    }
    // factor & inv_factor
    fac[0] = 1;
    rep(i,1,c) fac[i] = mul(fac[i - 1], i);
    invF[c] = qp(fac[c], mod - 2);
    per(i,c - 1,0) invF[i] = mul(invF[i + 1], i + 1);
    // build cartesian tree
    stack<int> stk;
    rep(x,1,n) {
        int lst = 0;
        while(!stk.empty() && a[stk.top()] > a[x]) lst = stk.top(), stk.pop();
        if(stk.empty()) root = x;
        else rs[stk.top()] = x;
        ls[x] = lst;
        stk.push(x);
    }
    f[0][0] = 1;
    dfs(root, 0);
    printf("%d\n", f[root][k]);
    return 0;
}

Solution

我们发现若我们在 $t$ 时刻从 $x$ 走到 $y$，我们可以在这一条边上反复横跳让我们在 $t + 2,~t + 4,~\dots$ 时刻均能到达 $y$，直到该边消失。由于这些能到达 $y$ 的时刻奇偶性均相同，因此考虑将每个点拆分为两个，一个为奇点一个为偶点，每次到达奇点时的时刻为奇数，到达偶点的时刻为偶数。对于一条 $x$ 向 $y$ 的边，拆点后即为 $x$ 的奇点向 $y$ 的偶点连边和 $x$ 的偶点向 $y$ 的奇点连边。

考虑在拆完点后得到的图上跑最短路，但是将最短路状态记在点上是不妥的，因为点是不会消失的，因此无法判断长于最短路的某一个路径长度是否合法。考虑将最短路状态记在边上，对每条有向边记录其最早的到达这条边起点的时间。到达一个点的最早时间即为他的所有入边的最短路的最小值加一。

Code

View On GitHub

/**
 * @file 827F.cpp
 * @author Macesuted (i@macesuted.moe)
 * @date 2022-04-03
 *
 * @copyright Copyright (c) 2022
 * @brief
 *      My Tutorial: https://macesuted.moe/article/cf827f
 *
 */

#include <bits/stdc++.h>
using namespace std;

namespace IO {
const int SIZE = 1 << 20;
char Ibuf[SIZE], *Il = Ibuf, *Ir = Ibuf, Obuf[SIZE], *Ol = Obuf, *Or = Ol + SIZE - 1;
int cache1[100], cache2[100];
char isspace(char c) { return c == ' ' || c == '\t' || c == '\n' || c == '\v' || c == '\f' || c == '\r'; }
char iseoln(char c) { return c == '\n' || c == '\r'; }
void fill(void) { return Ir = (Il = Ibuf) + fread(Ibuf, 1, SIZE, stdin), void(); }
void flush(void) { return fwrite(Obuf, 1, Ol - Obuf, stdout), Ol = Obuf, void(); }
char buftop(void) { return Ir == Il && (fill(), 1), *Il; }
char getch(void) { return Il == Ir ? fill(), Il == Ir ? EOF : *Il++ : *Il++; }
void putch(char x) { return *Ol++ = x, Ol == Or && (flush(), 1), void(); }
template <typename T = int>
T read(void) {
    T x = 0, f = +1;
    char c = getch();
    while (c < '0' || c > '9') (c == '-') && (f = -f), c = getch();
    while ('0' <= c && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48), c = getch();
    return x * f;
}
template <typename T>
void write(T x) {
    if (!x) return putch('0');
    if (x < 0) putch('-'), x = -x;
    int top = 0;
    while (x) cache1[top++] = x % 10, x /= 10;
    while (top) putch(cache1[--top] ^ 48);
    return;
}
template <typename T>
void writeDouble(T x, int dep = 10) {
    if (x < 0) putch('-'), x = -x;
    int64_t fx = x;
    x -= fx;
    for (int i = 0; i < dep; i++) cache2[i] = (x *= 10), x -= int(x);
    if (int(x * 10) > 4) {
        cache2[dep - 1]++;
        for (int i = dep - 1; i; i--)
            if (cache2[i] == 10) cache2[i] = 0, cache2[i - 1]++;
        if (cache2[0] == 10) cache2[0] = 0, fx++;
    }
    write(fx), putch('.');
    for (int i = 0; i < dep; i++) putch(cache2[i] ^ 48);
    return;
}
string getstr(const string& suf = "") {
    string s = suf;
    while (isspace(buftop())) getch();
    for (char* p = Il; Il != Ir; fill(), p = Il) {
        while (Il < Ir && !isspace(*Il) && *Il != EOF) Il++;
        s.append(p, Il);
        if (Il < Ir) break;
    }
    return s;
}
string getline(const string& suf = "") {
    string s = suf;
    while (iseoln(buftop())) getch();
    for (char* p = Il; Il != Ir; fill(), p = Il) {
        while (Il < Ir && !iseoln(*Il) && *Il != EOF) Il++;
        s.append(p, Il);
        if (Il < Ir) break;
    }
    return s;
}
void putstr(string str, int begin = 0, int end = -1) {
    if (end == -1) end = str.size();
    for (int i = begin; i < end; i++) putch(str[i]);
    return;
}
struct Flusher_ {
    ~Flusher_() { flush(); }
} io_flusher_;
}  // namespace IO
using IO::getch;
using IO::getline;
using IO::getstr;
using IO::putch;
using IO::putstr;
using IO::read;
using IO::write;
using IO::writeDouble;

bool mem1;

#define maxn 500005

typedef tuple<int, int, int> tiii;

vector<vector<tiii>> graph;
vector<vector<tiii>::iterator> cur;
int dist[maxn];

void addEdge(int x, int y, int l, int r) {
    return l <= r &&
               (graph[x].emplace_back(l + (l & 1), r - (r & 1), y), graph[y].emplace_back(l + !(l & 1), r - !(r & 1), x), 1),
           void();
}

void solve(void) {
    int n = read(), m = read();
    graph.resize(2 * n + 1), cur.resize(2 * n + 1);
    for (int i = 1; i <= m; i++) {
        int x = read(), y = read(), l = read(), r = read() - 1;
        addEdge(x, y + n, l, r), addEdge(y, x + n, l, r);
    }
    for (int i = 1; i <= 2 * n; i++) sort(cur[i] = graph[i].begin(), graph[i].end());
    memset(dist, 0x3f, sizeof(dist)), dist[1] = 0;
    static priority_queue<tiii, vector<tiii>, greater<tiii>> que;
    while (!que.empty()) que.pop();
    while (cur[1] != graph[1].end() && get<0>(*cur[1]) == 0) que.emplace(1, get<1>(*cur[1]) + 1, get<2>(*cur[1])), cur[1]++;
    while (!que.empty()) {
        auto [l, r, x] = que.top();
        que.pop(), dist[(x - 1) % n + 1] = min(dist[(x - 1) % n + 1], l);
        for (auto& i = cur[x]; i != graph[x].end() && get<0>(*i) <= r; i++)
            if (get<1>(*i) >= l) que.emplace(max(l, get<0>(*i)) + 1, get<1>(*i) + 1, get<2>(*i));
    }
    return write(dist[n] == 0x3f3f3f3f ? -1 : dist[n]), putch('\n');
}

bool mem2;

int main() {
    ios::sync_with_stdio(false);
#ifdef MACESUTED
    cerr << "Memory Cost: " << abs(&mem1 - &mem2) / 1024. / 1024. << "MB" << endl;
#endif

    int _ = 1;
    while (_--) solve();

#ifdef MACESUTED
    cerr << "Time Cost: " << clock() * 1000. / CLOCKS_PER_SEC << "MS" << endl;
#endif
    return 0;
}

设 $N = kM + r$ , 对于满足题意的 $M$ 有 $M = rs$ ，其中 $s \neq 1$ 。

此时 $N = (ks + 1)r$ 。

对 $r \neq 1$ ，枚举 $r$ ，求 $\frac{N}{r} - 1$ 的非 $1$ 约数个数和即可。

对 $r = 0$ 实际上就是约数。

这种枚举是不漏的，因为我们对于每个 $r$ 求出了所有可能的 $M$ 。

这种枚举是不重的，首先每个 $M$ 对应唯一的 $r$ ，而对于每个 $r$ ，不同的 $s$ 又能得到不同的 $M$ 。

这种枚举的复杂度的表达式大概是

看起来是 $\mathcal{O}$ (能过) ，我在 vp 的时候对着那张约数个数级别表格看了好久一度以为很难过，实际上是不高于 $\mathcal{O}(\sqrt {N} \log N )$ 。而且随机数据下跑的非常快。

code

int test(ll x) {
    if(x == 0) return 0;
    int ret = 0;
    for(ll i = 1; i * i <= x; ++ i) {
        if(x % i == 0)
            ret += 2;
        if(x == i * i) -- ret;
    }
    return ret - 1;
}

int main() {
    ll n, ans = 0;
    scanf("%lld", &n);
    for(ll i = 1; i * i <= n; ++ i) {
        if(n % i != 0) continue;
        ll t = n / i;
        ans += test(i - 1) + 1;
        if(n == i * i) continue;
        ans += test(t - 1) + 1;
    }
    printf("%lld\n", ans);
    return 0;
}

关于复杂度

约数和函数：

这个东西在 $k < 1$ 的时候的阶的估计大概是这样的：

感觉这个东西没有初阶的证明方法。

姑且认为 $\sum_{d \mid n} \sqrt d \sim \mathcal{O}(\sqrt n \log n)$ 。

Solution

交互题考虑分析操作和规模，对于 $\texttt{B}$ 操作，我们发现如果 $a$ 的倍数中有 $x$，那么最后删除的时候是不会删除 $x$ 的，但是我们又可以使用 $\texttt{A}$ 操作来得到集合中 $a$ 的倍数。

如果 $x$ 不是 $a$ 的倍数，那么使用 $\texttt{B}$ 操作之后再使用一次 $\texttt{A}$ 操作得到的回复应该是 $0$，否则为 $1$。

因此，我们有了一种暴力的思路，我们考虑对于 $10^5$ 内所有质数，都执行一遍上面的操作，然后我们可以确定出 $x$ 是由哪些质因子构成的，然后最后我们再询问这些质因子的次幂即可。

那么，这么做的操作次数为多少呢？

$10^5$ 范围内的质数有 $9592$ 个，我们至少对每个质数都执行了两遍操作，然后还有最后找出数 $x$ 又需要一些次数，超出规定的 $10^4$ 操作次数。

考虑优化我们的交互策略，对质数进行根号分治。

将大于 $316$ 的质数和小于 $316$ 的质数分别进行处理。

对于大于 $316$ 的质数，任何 $x$ 都最多只会有一个 $1$ 这么的质因数出现，否则就超出了值域 $10^5$。

对于小于 $316$ 的质数，只有 $65$ 个质数。

对于这些质数，我们先进行之前的策略，得到 $x$ 的小质数因子，并且询问出他应有的次幂。

可以计算出，这部分操作次数最多为 $238$ 次。

然后执行完之后只会有 $1,x$ 和 $x$ 的大质数因子。

然后对于大质数，还拥有 $9527$ 个。

假设之前得到的小质数因子乘积 $d$ 大于 $1$。

那么这个数是个合数，直接询问所有大质数 $p\times d$ 是否存在，如果存在那么 $x = p \times d$ 。

这部分的操作次数最多为 $238+9527+1=9766$。

如果 $d=1$ 的话，那么证明我们的数 $x$ 是个质数或者为 $1$，他就在后面的大质数因子中。

那么不能照搬上面的做法了，而直接暴力操作次数要乘二，就超了。

人类智慧，接下来的序列中只有 $1$ 和大质数。

对大质数进行分块，每 $100$ 个大质数分一块，每次连续删 $100$ 个大质数。

然后询问 $\texttt{A 1}$ 可以得到现在序列中数量，按理来说应该是每次减少 $100$ 个，如果有一次减少的是 $99$ 个，证明 $x$ 在这一块中，然后暴力递归找即可。

这部分的操作次数最终也不会超过 $10^4$ 。

实际上我调了一下块长为 $86$，因为我写丑了。

Code

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
#include <bits/stdc++.h>
#define int long long
using namespace std;
#define FOR(i, l, r) for(int i = (l); i <= r; ++i)
#define REP(i, l, r) for(int i = (l); i <  r; ++i)
#define DFR(i, l, r) for(int i = (l); i >= r; --i)
#define DRP(i, l, r) for(int i = (l); i >  r; --i)
#define FORV(i, ver) for(int i = 0; i < ver.size(); i++)
#define FORP(i, ver) for(auto i : ver)
template<class T>T wmin(const T &a, const T &b) {return a < b ? a : b;}
template<class T>T wmax(const T &a, const T &b) {return a > b ? a : b;}
template<class T>bool chkmin(T &a, const T &b) {return a > b ? a = b, 1 : 0;}
template<class T>bool chkmax(T &a, const T &b) {return a < b ? a = b, 1 : 0;}
inline int read() {
  int x = 0, f = 1;  char ch = getchar();
  while( !isdigit(ch) ) { if(ch == '-') f = -1;  ch = getchar();  }
  while( isdigit(ch) ) {  x = (x << 1) + (x << 3) + (ch ^ 48);  ch = getchar();  }
  return x * f;
}
const int N = 2e6;
int n, vis[N], pr[N], tot, c[N], num;
void prime(int n) {
  FOR (i, 2, n) {
    if (vis[i]) continue;
    pr[++tot] = i;
    for (int j = i; j <= n; j += i) vis[j] = 1;
  }
}
int A(int x) {
  cout << "A " << x << "\n";  cout.flush();
  int qwq;  cin >> qwq;  return qwq;
}
void B(int x) {
  cout << "B " << x << "\n";  cout.flush();
  int qwq;  cin >> qwq;
}
void C(int x) {
  cout << "C " << x << "\n";  cout.flush();  exit(0);
}
signed main () {
  ios::sync_with_stdio(0);
  cin.tie(0), cout.tie(0);
  n = read(); prime(n);
  if (n == 1) { C(1); }
  int now = 1;
  FOR (i, 1, tot) {
    if (pr[i] > 316) break;
    int x = pr[i];
    B(x);
    if ( A(x) == 1 ) {
      now = now * x;
      int gtr = x;
      while (1) {
        gtr *= x;
        if (gtr > n) break;
        if ( A(gtr) == 1 ) now *= x;
        else break;
      }
    }
  }
  if (now == 1) {
    int ans = 1;
    FOR (i, 1, tot) {
      if (pr[i] < 316) continue;
      c[++num] = pr[i];
    }
    int siz = 86, bel = (num - 1) / siz + 1;
    int cnt = A(1);
    FOR (i, 1, bel) {
      int l = (i - 1) * siz + 1;
      int r = wmin(num, i * siz);
      int len = r - l + 1;
      FOR (j, l, r) {
        int x = c[j];
        B(x);
      }
      int qaq = A(1);
      if (qaq == cnt - len) { cnt -= len;  continue;  }
      FOR (j, l, r) {
        int x = c[j];
        int qwq = A(x);
        if (qwq) C(x);
      }
    }
    C(1);
  }
  FOR (i, 1, tot) {
    if (pr[i] < 316) continue;
    int x = pr[i];
    if (x * now > n) break;
    if (A(x * now) == 1) C(x * now);
  }
  C(now);
  return 0;
}

Solution

我们显然无法使用平衡树直接维护每个点的单点信息，因为题目中给出的操作对于区间中的每一个元素均与它两边的元素进行了运算，难以直接维护每个单点的信息。

所以我们考虑将原序列拆分为一些区间，使之可以较方便地处理题目中给出的这些操作。

一个比较显然的想法是将原序列拆分为若干段同色的极长段。比如将 $0,~1,~1,~0,~0,~1$ 划分为 $[0]~[1,~1]~[0,~0]~[1]$。容易发现这样划分之后，如果一个操作覆盖了某一个区间，我们可以方便地计算出该操作对该区间的影响：

• 1 操作： 所覆盖的 1 区间均变为 0 区间。
• 2 操作： 所覆盖的 0 区间均变为 1 区间。
• 3 操作： 所覆盖的 0 区间右端点 $-1$，所覆盖的 1 区间左端点 $-1$。
• 4 操作： 所覆盖的 0 区间左端点 $+1$，所覆盖的 1 区间右端点 $+1$。
• 5 操作： 所覆盖的 0 区间左端点 $-1$，所覆盖的 1 区间右端点 $-1$。
• 6 操作： 所覆盖的 0 区间右端点 $+1$，所覆盖的 1 区间左端点 $+1$。

同时，由于我们需要在下放标记前计算出某个询问区间对应的元素和，所以我们需要保证每一个区间均为极长区间，也就是不能让空区间留在平衡树中。

由于在整个过程中于平衡树上出现的区间数量是 $O(n+m)$ 级别的，所以我们可以在每个平衡树结点上记录其子树内最短的 0/1 区间的长度，在该长度达到 0 时暴力地向下搜索找到空区间并删除，对于每个空区间我们需要花费 $O(\log n)$ 的时间复杂度，因此总共花费在删除空区间操作上的时间是 $O((n+m)\log n)$ 级别的，可以接受。

根据上面提到的方法维护平衡树即可。

Code

编写代码用时 3h，调试用时 2h，使用指针版 FhqTreap，由于卡常使用了内存池并省去了回收内存操作。

下面是一些注意事项和建议：

• 写代码时务必多画图，仔细考虑每一个操作的边界情况。（即操作区间的左右端点所在区间是否需要被修改的情况）
• 由于代码较长建议每写完几个操作就进行简单的测试以检验其正确性。
• 如果 WA 并且找不到显然的错误，可以在每次操作结束后输出整棵平衡上的所有区间的信息，配合手动模拟或是暴力代码测试几组数据。

View on GitHub

/**
 * @author Macesuted (i@macesuted.moe)
 * @copyright Copyright (c) 2021
 * @brief
 *      My solution: https://www.macesuted.cn/article/lg5066/
 */

#include <bits/stdc++.h>
using namespace std;

namespace io {
#define SIZE (1 << 20)
char ibuf[SIZE], *iS, *iT, obuf[SIZE], *oS = obuf, *oT = oS + SIZE - 1, c, qu[55];
int f, qr;
inline void flush(void) { return fwrite(obuf, 1, oS - obuf, stdout), oS = obuf, void(); }
inline char getch(void) { return (iS == iT ? (iT = (iS = ibuf) + fread(ibuf, 1, SIZE, stdin), (iS == iT ? EOF : *iS++)) : *iS++); }
inline void putch(char x) {
    *oS++ = x;
    if (oS == oT) flush();
    return;
}
string getstr(void) {
    string s = "";
    char c = getch();
    while (c == ' ' || c == '\n' || c == '\r' || c == '\t' || c == EOF) c = getch();
    while (!(c == ' ' || c == '\n' || c == '\r' || c == '\t' || c == EOF)) s.push_back(c), c = getch();
    return s;
}
void putstr(string str, int begin = 0, int end = -1) {
    if (end == -1) end = str.size();
    for (register int i = begin; i < end; i++) putch(str[i]);
    return;
}
template <typename T>
inline T read() {
    register T x = 0;
    for (f = 1, c = getch(); c < '0' || c > '9'; c = getch())
        if (c == '-') f = -1;
    for (x = 0; c <= '9' && c >= '0'; c = getch()) x = x * 10 + (c & 15);
    return x * f;
}
template <typename T>
inline void write(const T& t) {
    register T x = t;
    if (!x) putch('0');
    if (x < 0) putch('-'), x = -x;
    while (x) qu[++qr] = x % 10 + '0', x /= 10;
    while (qr) putch(qu[qr--]);
    return;
}
struct Flusher_ {
    ~Flusher_() { flush(); }
} io_flusher_;
}  // namespace io
using io::getch;
using io::getstr;
using io::putch;
using io::putstr;
using io::read;
using io::write;

#define maxn 3000005
#define INF 0x3f3f3f3f

class FhqTreap {
   private:
    struct Node {
        int rank;
        int col;             // 区间颜色
        int sum;             // 子树和
        int siz[2];          // 子树内 0/1 区间数量
        int tl, tr;          // 区间左右端点
        int deltaL, deltaR;  // 1 区间左右端点偏移量
        int minLen[2];       // 子树内最短 0/1 区间长度
        Node *l, *r;         // 平衡树左右孩子
        Node(void) {}
        Node(int _rank, int _col, int _tl, int _tr) {
            rank = _rank;
            col = _col;
            tl = _tl, tr = _tr;
            l = r = NULL;
            reset();
        }
        // 重新计算该点的单点信息
        void reset(void) {
            siz[col] = 1, siz[!col] = 0;
            sum = col * (tr - tl + 1);
            deltaL = deltaR = 0;
            minLen[col] = tr - tl + 1, minLen[!col] = INF;
            return;
        }
        Node operator+(const Node& b) const {
            Node a = *this;
            a.sum += b.sum;
            a.siz[0] += b.siz[0], a.siz[1] += b.siz[1];
            a.minLen[0] = min(a.minLen[0], b.minLen[0]), a.minLen[1] = min(a.minLen[1], b.minLen[1]);
            return a;
        }
    };

    Node pool[10000000];
    int tail = 0;

    Node* root;
    queue<Node*> needErase;  // 需要被删除的结点

    static const long long kMul = 0x9ddfea08eb382d69ULL;
    long long Seed = 1145141919810;
    inline long long fingerPrint(long long x) {
        return x *= kMul, x ^= x >> 47, x *= kMul, x ^= x >> 47, x *= kMul, x ^= x >> 47, x * kMul;
    }
    inline int frand(void) { return Seed += fingerPrint(Seed); }

    inline Node* newNode(int val, int l, int r) { return &(pool[tail++] = Node(frand(), val, l, r)); }

    inline void update(Node* p, int dl, int dr) {
        if (p == NULL) return;
        p->deltaL += dl, p->deltaR += dr;
        p->minLen[0] -= dl + dr, p->minLen[1] += dl + dr;
        p->sum += (dl + dr) * p->siz[1];
        if (p->col == 1)
            p->tl -= dl, p->tr += dr;
        else
            p->tl += dr, p->tr -= dl;
        return;
    }
    void findEmpty(Node* p) {
        if (p == NULL) return;
        if (p->minLen[0] && p->minLen[1]) return;
        pushDown(p);
        if (p->tl > p->tr) needErase.push(p);
        findEmpty(p->l), findEmpty(p->r);
        return;
    }
    void eraseEmpty(void) {
        while (!needErase.empty()) {
            Node* p = needErase.front();
            needErase.pop();
            Node *nodeL = NULL, *treeM = NULL, *nodeR = NULL, *treeR = NULL;
            split1(root, root, treeR, p->tl - 1), split1(treeR, treeM, treeR, p->tl);
            split2(root, root, nodeL, p->tl - 2);
            if (p == treeM)
                nodeR = (p->l == NULL) ? p->r : p->l;
            else
                nodeR = treeM, nodeR->l = nodeR->r = NULL;
            // delete p;
            if (nodeL != NULL && nodeR != NULL) nodeL->tr = nodeR->tr, nodeL->reset(), /* delete nodeR, */ nodeR = NULL;
            merge(root, root, nodeL), merge(root, root, nodeR), merge(root, root, treeR);
        }
        return;
    }
    // void destroy(Node* p) {
    //     if (p == NULL) return;
    //     if (p->l != NULL) destroy(p->l);
    //     if (p->r != NULL) destroy(p->r);
    //     delete p;
    //     return;
    // }
    void pushDown(Node* p) {
        if (!p->deltaL && !p->deltaR) return;
        if (p->l != NULL) update(p->l, p->deltaL, p->deltaR);
        if (p->r != NULL) update(p->r, p->deltaL, p->deltaR);
        p->deltaL = p->deltaR = 0;
        return;
    }
    inline void pushUp(Node* p) {
        p->reset();
        if (p->l != NULL) *p = *p + *(p->l);
        if (p->r != NULL) *p = *p + *(p->r);
        return;
    }

    // 将对应区间左端点 <= p 的部分划分到 tree1，左端点 > p 的部分划分到 tree2
    void split1(Node* root, Node*& tree1, Node*& tree2, int p) {
        if (root == NULL) return tree1 = tree2 = NULL, void();
        pushDown(root);
        if (root->tl <= p)
            tree1 = root, split1(root->r, tree1->r, tree2, p);
        else
            tree2 = root, split1(root->l, tree1, tree2->l, p);
        return pushUp(root);
    }
    // 将对应区间右端点 <= p 的部分划分到 tree1，右端点 > p 的部分划分到 tree2
    void split2(Node* root, Node*& tree1, Node*& tree2, int p) {
        if (root == NULL) return tree1 = tree2 = NULL, void();
        pushDown(root);
        if (root->tr <= p)
            tree1 = root, split2(root->r, tree1->r, tree2, p);
        else
            tree2 = root, split2(root->l, tree1, tree2->l, p);
        return pushUp(root);
    }
    void merge(Node*& root, Node* tree1, Node* tree2) {
        if (tree1 == NULL) return root = tree2, void();
        if (tree2 == NULL) return root = tree1, void();
        if (tree1->rank < tree2->rank)
            pushDown(root = tree1), merge(root->r, tree1->r, tree2);
        else
            pushDown(root = tree2), merge(root->l, tree1, tree2->l);
        return pushUp(root);
    }

    void print(Node* root) {
        if (root == NULL) return;
        pushDown(root);
        if (root->l != NULL) print(root->l);
        cerr << '[' << root->tl << '~' << root->tr << ':' << root->col << ']';
        if (root->r != NULL) print(root->r);
        return;
    }

   public:
    FhqTreap(void) { root = NULL; }
    void pushBack(int l, int r, int val) {
        Node* p = newNode(val, l, r);
        merge(root, root, p);
        return;
    }
    void opt1_2(int l, int r, int val) {
        Node *nodeL = NULL, *p = NULL, *nodeR = NULL, *treeR = NULL;
        split2(root, root, p, l - 1), split1(p, p, treeR, r);
        split1(p, nodeL, p, l - 1), split2(p, p, nodeR, r);
        if (nodeL != NULL) {
            if (nodeL->tr > r) nodeR = newNode(nodeL->col, r, nodeL->tr);
            nodeL->tr = l - 1, nodeL->reset();
        } else
            split2(root, root, nodeL, l - 2);
        if (nodeR != NULL)
            nodeR->tl = r + 1, nodeR->reset();
        else
            split1(treeR, nodeR, treeR, r + 1);
        // destroy(p);
        p = newNode(val, l, r);
        if (nodeL != NULL && p->col == nodeL->col) {
            p->tl = nodeL->tl, p->reset();
            // delete nodeL;
            nodeL = NULL;
        }
        if (nodeR != NULL && p->col == nodeR->col) {
            p->tr = nodeR->tr, p->reset();
            // delete nodeR;
            nodeR = NULL;
        }
        merge(root, root, nodeL), merge(root, root, p), merge(root, root, nodeR), merge(root, root, treeR);
        return;
    }
    void opt3(int l, int r) {
        r--;
        Node *treeM = NULL, *treeR = NULL, *node = NULL;
        split2(root, root, treeM, l - 1), split1(treeM, treeM, treeR, r);
        split1(treeM, node, treeM, l);
        if (node != NULL && node->col == 1)
            merge(root, root, node);
        else
            merge(treeM, node, treeM);
        node = NULL;
        split2(treeM, treeM, node, r - 1);
        if (node != NULL && node->col == 0) {
            if (node->tr > r)
                merge(treeR, node, treeR);
            else {
                merge(treeM, treeM, node);
                Node* nodeR = NULL;
                split1(treeR, nodeR, treeR, r + 1);
                merge(treeM, treeM, nodeR);
            }
        } else
            merge(treeM, treeM, node);
        if (treeM != NULL) update(treeM, 1, 0);
        merge(root, root, treeM), merge(root, root, treeR);
        findEmpty(root), eraseEmpty();
        return;
    }
    void opt4(int l, int r) {
        l++;
        Node *treeM = NULL, *treeR = NULL, *node = NULL;
        split2(root, root, treeM, l - 1), split1(treeM, treeM, treeR, r);
        split1(treeM, node, treeM, l);
        if (node != NULL && node->col == 0) {
            if (node->tl < l)
                merge(root, root, node);
            else {
                merge(treeM, node, treeM);
                Node* nodeL = NULL;
                split2(root, root, nodeL, l - 2);
                merge(treeM, nodeL, treeM);
            }
        } else
            merge(treeM, node, treeM);
        node = NULL;
        split2(treeM, treeM, node, r - 1);
        if (node != NULL && node->col == 1)
            merge(treeR, node, treeR);
        else
            merge(treeM, treeM, node);
        if (treeM != NULL) update(treeM, 0, 1);
        merge(root, root, treeM), merge(root, root, treeR);
        findEmpty(root), eraseEmpty();
        return;
    }
    void opt5(int l, int r) {
        r--;
        Node *treeM = NULL, *treeR = NULL, *node = NULL;
        split2(root, root, treeM, l - 1), split1(treeM, treeM, treeR, r);
        split1(treeM, node, treeM, l);
        if (node != NULL && node->col == 0)
            merge(root, root, node);
        else
            merge(treeM, node, treeM);
        node = NULL;
        split2(treeM, treeM, node, r - 1);
        if (node != NULL && node->col == 1) {
            if (node->tr > r)
                merge(treeR, node, treeR);
            else {
                merge(treeM, treeM, node);
                Node* nodeR = NULL;
                split1(treeR, nodeR, treeR, r + 1);
                merge(treeM, treeM, nodeR);
            }
        } else
            merge(treeM, treeM, node);
        if (treeM != NULL) update(treeM, 0, -1);
        merge(root, root, treeM), merge(root, root, treeR);
        findEmpty(root), eraseEmpty();
        return;
    }
    void opt6(int l, int r) {
        l++;
        Node *treeM = NULL, *treeR = NULL, *node = NULL;
        split2(root, root, treeM, l - 1), split1(treeM, treeM, treeR, r);
        split1(treeM, node, treeM, l);
        if (node != NULL && node->col == 1) {
            if (node->tl < l)
                merge(root, root, node);
            else {
                merge(treeM, node, treeM);
                Node* nodeL = NULL;
                split2(root, root, nodeL, l - 2);
                merge(treeM, nodeL, treeM);
            }
        } else
            merge(treeM, node, treeM);
        node = NULL;
        split2(treeM, treeM, node, r - 1);
        if (node != NULL && node->col == 0)
            merge(treeR, node, treeR);
        else
            merge(treeM, treeM, node);
        if (treeM != NULL) update(treeM, -1, 0);
        merge(root, root, treeM), merge(root, root, treeR);
        findEmpty(root), eraseEmpty();
        return;
    }
    int opt7(int l, int r) {
        Node *node = NULL, *p = NULL, *treeR = NULL;
        split2(root, root, p, l - 1), split1(p, p, treeR, r);
        int answer = 0;
        if (p != NULL) answer += p->sum;
        split1(p, node, p, l - 1);
        if (node != NULL) answer -= node->col * (l - node->tl);
        merge(p, node, p);
        node = NULL;
        split2(p, p, node, r);
        if (node != NULL) answer -= node->col * (node->tr - r);
        merge(p, p, node);
        merge(root, root, p), merge(root, root, treeR);
        return answer;
    }
    inline void print(void) { return print(root), cerr << endl, void(); }
};

FhqTreap treap;

int a[maxn];

int main() {
    int n = read<int>(), m = read<int>();
    for (register int i = 1; i <= n; i++) a[i] = read<int>();
    int last = 1;
    for (register int i = 2; i <= n; i++)
        if (a[i] != a[i - 1]) treap.pushBack(last, i - 1, a[i - 1]), last = i;
    treap.pushBack(last, n, a[n]);
    last = 0;
    while (m--) {
        int opt = read<int>(), l = last ^ read<int>(), r = last ^ read<int>();
        if (opt == 1)
            treap.opt1_2(l, r, 0);
        else if (opt == 2)
            treap.opt1_2(l, r, 1);
        else if (opt == 3)
            treap.opt3(l, r);
        else if (opt == 4)
            treap.opt4(l, r);
        else if (opt == 5)
            treap.opt5(l, r);
        else if (opt == 6)
            treap.opt6(l, r);
        else
            write(last = treap.opt7(l, r)), putch('\n');
    }
    return 0;
}

Solution

由于 $l_i \le p \le l_i + len$ 与 $p - len + 1 \le l_i \le p$ 相同，因此在固定询问线段长度 $len$ 的情况下，可以将原问题中的询问线段变为位置在 $l_i$ 上的单点，$m$ 个点变为 $[p - len + 1,~p]$ 的线段，问题即转换为求移动该点使其依次经过每个区间的最短总距离。

结论 1：在一种移动方案中，若 $i - 1$ 时刻向 $i$ 时刻移动的方向与 $i$ 时刻向 $i + 1$ 时刻移动的方向相同，则 $i$ 时刻的限制可以无视。

证明：令 $i$ 时刻点所在位置为 $p_i$，以向右移动为例则若条件满足则说明 $p_{i - 1} < p_i < p_{i + 1}$。固定 $p_{i - 1}$ 和 $p_{i + 1}$ 时所有在该两点间的移动方案总会经过 $p_i$，在经过 $p_i$ 时满足 $i$ 时刻限制即可。

结论 2：若两个相邻限制线段 $[l_i,~r_i]$，$[l_{i + 1},~r_{i + 1}]$ 有交，则这两条线段的限制条件与一条 $[\max(l_i,~l_{i + 1}),~\min(r_i,~r_{i + 1})]$ 线段相同。

证明：$p_i$ 向 $p_{i + 1}$ 移动的过程中必定会经过他们交线段上的至少一个点，因此满足两条线段限制条件的方案必定满足交线段的限制条件。所有满足交线段限制条件的方案显然满足 $i$ 时刻和 $i + 1$ 时刻的限制，因此满足交线段限制条件的方案必定满足原来的两条线段的限制条件。

当我们固定询问区间长度 $len$ 时，通过结论 2 的约束，我们可以使得最终限制条件中任意两条相邻线段均不交。因此我们能够确定每一条线段（除了最后一条），该线段与下一条线段之间的移动方向。

结论 3：对于线段 $i$，若其到线段 $i + 1$ 的移动方向为左，则线段 $i$ 的限制条件与 $[l_i,~l_i]$ 相同。

证明显然，根据贪心，离下一条线段最近的点必然不劣。

根据结论 3，我们可以把所有线段限制缩为点，问题转化为：询问一点与 $m$ 个给定点依次相交的移动路径和。我们令第 $i$ 个限制为 $lim_i$。

根据结论 1，我们发现若出现 $lim_{i - 1} < lim_i < lim_{i + 1}$ 的情况，则 $lim_i$ 将不会起约束作用。我们按上述限制删除无用限制后，发现限制总是满足： $lim_{i - 1} < lim_i > lim_{i + 1}$ 或 $lim_{i - 1} > lim_i < lim_{i + 1}$。此时询问 $q$ 的答案即为 $|lim_1 - l_q| + \sum_{i = 1}^{m - 1} | lim_i - lim_{i + 1} |$。

在固定 $len$ 的情况下我们已经能够求解原问题了，考虑在不固定 $len$ 时我们应该怎么做。我们考虑将所有询问离线后按照 $len$ 排序，从小到达枚举 $len$ 的同时维护限制条件下对应的答案。

我们可以将所有 $lim$ 分为左右两半，满足 $lim_{i - 1} > lim_i < lim_{i + 1}$ 的为左点，满足 $lim_{i - 1} < lim_i > lim_{i + 1}$ 的为右点。最终移动路径上的点一定为左右点相邻。所有的左点为原区间的右端点，所有的右点为原区间的左端点。由于原区间为 $[p - len + 1,~p]$，在 $len$ 增大时左端点会向左移动，即所有右点在 $len$ 增大 $1$ 时会向左移动 $1$。因此在询问的 $len$ 增大时我们只要给全局所有的右点通过懒标记整体向左移即可。

但是由于右点向左移动最终会与左点相交，相交后根据结论 2 我们需要删除相交的两个点中的一个，删除一个点后会出现两个同类点相邻的情况，令未删除的点为 $x$。当 $x$ 为第一个限制或是最后一个限制时令 $x$ 从左点变为右点或是从右点变为左点，$x$ 不为第一个或最后一个时删除 $x$ 因为其值在 $x - 1$ 与 $x + 1$ 之间。上述操作完后即可重新回到正常状态。

令相邻两限制间的距离为他们初始时刻的距离，使用 $set$ 维护所有相邻两限制间的距离，处理时间 $tim$ 时将所有距离不超过 $tim$ 的限制按照上述操作处理即可。由于每个时刻相邻两限制间的距离都会减一，因此最终答案即为 $|lim_1 - l_q| + \sum_{i = 1}^{m - 1} | lim_i - lim_{i + 1} | - (m - 1) \times tim$。全局维护相邻限制距离和即可。

需要注意的是当只剩下一个限制时，由于不存在所谓“下一步移动方向”，随时间推移该点会逐渐展开为线段。

时间复杂度 $O(n \log n)$，常数较大。

Code

View on GitHub

/**
 * @file 4249.cpp
 * @author Macesuted (i@macesuted.moe)
 * @date 2022-03-25
 *
 * @copyright Copyright (c) 2022
 * @brief
 *      My Tutorial: https://macesuted.moe/article/bzoj4249
 *
 */

#include <bits/stdc++.h>
using namespace std;

namespace IO {
const int SIZE = 1 << 20;
char Ibuf[SIZE], *Il = Ibuf, *Ir = Ibuf, Obuf[SIZE], *Ol = Obuf, *Or = Ol + SIZE - 1, stack[32];
char isspace(char c) { return c == ' ' || c == '\t' || c == '\n' || c == '\v' || c == '\f' || c == '\r'; }
void fill(void) { return Ir = (Il = Ibuf) + fread(Ibuf, 1, SIZE, stdin), void(); }
void flush(void) { return fwrite(Obuf, 1, Ol - Obuf, stdout), Ol = Obuf, void(); }
char buftop(void) { return Ir == Il ? fill(), *Il : *Il; }
char getch(void) { return Il == Ir ? fill(), Il == Ir ? EOF : *Il++ : *Il++; }
void putch(char x) { return *Ol++ = x, Ol == Or ? flush() : void(); }
template <typename T>
T read(void) {
    T x = 0, f = +1;
    char c = getch();
    while (c < '0' || c > '9') c == '-' ? void(f = -f) : void(), c = getch();
    while ('0' <= c && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48), c = getch();
    return x * f;
}
template <typename T>
void write(T x) {
    if (!x) putch('0');
    if (x < 0) putch('-'), x = -x;
    int top = 0;
    while (x) stack[top++] = (x % 10) ^ 48, x /= 10;
    while (top) putch(stack[--top]);
    return;
}
string getstr(const string& suf = "") {
    string s = suf;
    while (isspace(buftop())) getch();
    while (Il != Ir) {
        char* p = Il;
        while (Il < Ir && !isspace(*Il) && *Il != EOF) Il++;
        s.append(p, Il);
        if (Il < Ir) break;
        fill();
    }
    return s;
}
void putstr(string str, int begin = 0, int end = -1) {
    if (end == -1) end = str.size();
    for (int i = begin; i < end; i++) putch(str[i]);
    return;
}
struct Flusher_ {
    ~Flusher_() { flush(); }
} io_flusher_;
}  // namespace IO
using IO::getch;
using IO::getstr;
using IO::putch;
using IO::putstr;
using IO::read;
using IO::write;

bool mem1;

#define maxn 200005

typedef pair<int, int> pii;

set<pii> S, Sd;
map<int, vector<pii>> ques;
int a[maxn];
long long ans[maxn], answer = 0;

template <typename T>
T dec(T a) {
    return --a;
}
template <typename T>
T inc(T a) {
    return ++a;
}
void insert(set<pii>::iterator p) {
    return answer += abs(p->second - inc(p)->second), Sd.emplace(abs(p->second - inc(p)->second), p->first), void();
}
void erase(set<pii>::iterator p) {
    return answer -= abs(p->second - inc(p)->second), Sd.erase({abs(p->second - inc(p)->second), p->first}), void();
}

void check(pii x, int tim) {
    auto p = S.find(x);
    if (p == S.begin() && p == dec(S.end())) return;
    if (p == S.begin()) {
        if (p->second == inc(p)->second) return S.erase(p), void();
        if (inc(p)->second < p->second) S.erase(p), p = S.emplace(x.first, x.second + tim).first;
        return insert(p);
    }
    if (p == dec(S.end())) {
        if (p->second == dec(p)->second) return S.erase(p), void();
        if (dec(p)->second < p->second) S.erase(p), p = S.emplace(x.first, x.second + tim).first;
        return insert(dec(p));
    }
    return insert(--S.erase(p));
}

void solve(void) {
    int n = read<int>(), m = read<int>();
    for (int i = 1; i <= n; i++) {
        int l = read<int>(), r = read<int>();
        ques[r - l].emplace_back(l, i);
    }
    for (int i = 1; i <= m; i++) S.emplace(i, a[i] = read<int>());
    for (auto i = ++S.begin(); inc(i) != S.end(); i++)
        if ((dec(i)->second < i->second) == (i->second < inc(i)->second) || dec(i)->second == i->second ||
            i->second == inc(i)->second)
            i = --S.erase(i);
    for (auto i = S.begin(); inc(i) != S.end(); i++)
        Sd.emplace(abs(i->second - inc(i)->second), i->first), answer += abs(i->second - inc(i)->second);
    int last = 0;
    while (!Sd.empty()) {
        int tim = Sd.begin()->first, ip = Sd.begin()->second;
        Sd.erase(Sd.begin());
        if (tim != last)
            for (auto i = ques.begin(); i != ques.end() && i->first < tim; i = ques.erase(i)) {
                int t = S.begin()->second;
                if (S.begin()->second > inc(S.begin())->second) t -= i->first;
                for (auto j : i->second) ans[j.second] = answer + abs(t - j.first) - 1LL * ((int)S.size() - 1) * i->first;
            }
        last = tim;
        auto p = S.lower_bound({ip, 0}), q = inc(p);
        erase(p);
        if (p->second > q->second) {
            if (p != S.begin()) erase(dec(p));
            q = S.erase(p);
            if (q != dec(S.end())) erase(q);
            check(*q, tim);
        } else {
            if (q != dec(S.end())) erase(q);
            p = --S.erase(q);
            if (p != S.begin()) erase(dec(p));
            check(*p, tim);
        }
    }
    for (auto i : ques)
        for (auto j : i.second)
            if (S.begin()->second - (i.first - last) <= j.first && j.first <= S.begin()->second)
                ans[j.second] = 0;
            else
                ans[j.second] = min(abs(S.begin()->second - j.first), abs(S.begin()->second - (i.first - last) - j.first));
    for (int i = 1; i <= n; i++) write(ans[i]), putch('\n');
    return;
}

bool mem2;

int main() {
    ios::sync_with_stdio(false);
#ifdef MACESUTED
    cerr << "Memory Cost: " << abs(&mem1 - &mem2) / 1024. / 1024. << "MB" << endl;
#endif

    int _ = 1;
    while (_--) solve();

#ifdef MACESUTED
    cerr << "Time Cost: " << clock() * 1000. / CLOCKS_PER_SEC << "MS" << endl;
#endif
    return 0;
}

Solution

对于有区间归零操作的问题，我们的常用方法是记录每个位置上次被清零的时间。考虑一个最简单的简化问题版本：所有操作均为全局操作（即 $l_i = 1,~r_i = n$）。此时每次询问时所有位置离上次清零的时间均相同，令该时间为 $t$，我们发现所有 $\frac {m_i} {r_i} \le t$ 的小马的魔法值都会达到上限 $m_i$，其他小马的魔法值则为 $r_i \times t$。因此我们可以将所有小马按照 $\frac {m_i} {r_i}$ 排序，二分找到序列中 $\le t$ 的最大位置 $p$，则 $\sum_{1 \le i \le p} m_i + t \times (\sum_{p < i \le n} r_i)$ 即为答案。

考虑在清零操作为全局而询问操作为区间时该怎么做，即想要求得 $i \in [l,~r],~\frac {m_i} {r_i} \le t$ 的所有元素的 $m_i$ 和与 $r_i$ 和。经典的静态二维数点问题，为降低复杂度可以在 $\frac {m_i} {r_i}$ 一维上进行可持久化。具体的，将所有小马的 $\frac {m_i} {r_i}$ 排序，可持久化线段树的第 $i$ 个版本中插入排序后的前 $i$ 个元素。则二维数点问题转换为在排序后的数组上二分找到最大的 $\le t$ 的位置，在其对应的版本上询问 $[l,~r]$ 区间信息，复杂度 $O(\log n)$。

再考虑原问题，若全局的清零时间不同时应该怎么做。发现使用珂朵莉树维护每个连续清零时间相同的连续段即可。因为每次修改后会将区间内的所有元素的清零时间归零，每次询问时暴力扫描的每一块在询问后会被合并为一块，因此全局暴力扫描的时间复杂度为珂朵莉上块数的总和，而每次操作最多只会新建两个块，因此复杂度得以保证。对于珂朵莉树上的每个连续段，由于段内清零时间相同，做上述的可持久化线段树上查询即可。

另外，一个比较好的处理初始值 $s_i$ 的方法是将第 $i$ 个小马的初始上次清零时间设为 $- \frac {s_i} {r_i}$。

总时间复杂度 $O((n + q) \log n)$。

Code

View on GitHub

/**
 * @file 453E.cpp
 * @author Macesuted (i@macesuted.moe)
 * @date 2022-03-20
 *
 * @copyright Copyright (c) 2022
 *
 */

#include <bits/stdc++.h>
using namespace std;

namespace IO {
const int SIZE = 1 << 20;
char Ibuf[SIZE], *Il = Ibuf, *Ir = Ibuf, Obuf[SIZE], *Ol = Obuf, *Or = Ol + SIZE - 1, stack[32];
char isspace(char c) { return c == ' ' || c == '\t' || c == '\n' || c == '\v' || c == '\f' || c == '\r'; }
void fill(void) { return Ir = (Il = Ibuf) + fread(Ibuf, 1, SIZE, stdin), void(); }
void flush(void) { return fwrite(Obuf, 1, Ol - Obuf, stdout), Ol = Obuf, void(); }
char buftop(void) { return Ir == Il ? fill(), *Il : *Il; }
char getch(void) { return Il == Ir ? fill(), Il == Ir ? EOF : *Il++ : *Il++; }
void putch(char x) { return *Ol++ = x, Ol == Or ? flush() : void(); }
template <typename T>
T read(void) {
    T x = 0, f = +1;
    char c = getch();
    while (c < '0' || c > '9') c == '-' ? void(f = -f) : void(), c = getch();
    while ('0' <= c && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48), c = getch();
    return x * f;
}
template <typename T>
void write(T x) {
    if (!x) putch('0');
    if (x < 0) putch('-'), x = -x;
    int top = 0;
    while (x) stack[top++] = (x % 10) ^ 48, x /= 10;
    while (top) putch(stack[--top]);
    return;
}
string getstr(const string& suf = "") {
    string s = suf;
    while (isspace(buftop())) getch();
    while (Il != Ir) {
        char* p = Il;
        while (Il < Ir && !isspace(*Il) && *Il != EOF) Il++;
        s.append(p, Il);
        if (Il < Ir) break;
        fill();
    }
    return s;
}
void putstr(string str, int begin = 0, int end = -1) {
    if (end == -1) end = str.size();
    for (int i = begin; i < end; i++) putch(str[i]);
    return;
}
struct Flusher_ {
    ~Flusher_() { flush(); }
} io_flusher_;
}  // namespace IO
using IO::getch;
using IO::getstr;
using IO::putch;
using IO::putstr;
using IO::read;
using IO::write;

bool mem1;

#define maxn 100005

typedef pair<long long, long long> pll;

class SegmentTree {
   private:
    struct Node {
        Node *l, *r;
        long long sumR, sumM;
        Node(void) { l = r = NULL, sumR = sumM = 0; }
    };

    vector<Node*> roots;
    int n;

    Node* newRoot(void) { return roots.push_back(roots.back()), roots.back(); }
    void exist(Node*& p, Node* o) {
        if (p != o && p != NULL) return;
        return p = new Node(), *p = *o, void();
    }
    void pushUp(Node* p) {
        p->sumR = p->sumM = 0;
        if (p->l != NULL) p->sumR += p->l->sumR, p->sumM += p->l->sumM;
        if (p->r != NULL) p->sumR += p->r->sumR, p->sumM += p->r->sumM;
        return;
    }
    pll merge(pll a, pll b) { return {a.first + b.first, a.second + b.second}; }
    void insert(Node*& p, Node* o, int l, int r, int qp, int vr, int vm) {
        if (o == NULL) p = o = new Node();
        exist(p, o);
        if (l == r) return p->sumR = vr, p->sumM = vm, void();
        int mid = (l + r) >> 1;
        qp <= mid ? insert(p->l, o->l, l, mid, qp, vr, vm) : insert(p->r, o->r, mid + 1, r, qp, vr, vm);
        return pushUp(p);
    }
    pll query(Node* p, int l, int r, int ql, int qr) {
        if (p == NULL) return {0, 0};
        if (ql <= l && r <= qr) return {p->sumR, p->sumM};
        int mid = (l + r) >> 1;
        if (qr <= mid) return query(p->l, l, mid, ql, qr);
        if (ql > mid) return query(p->r, mid + 1, r, ql, qr);
        return merge(query(p->l, l, mid, ql, qr), query(p->r, mid + 1, r, ql, qr));
    }

   public:
    SegmentTree(void) { roots.push_back(NULL); }
    void resize(int _n) { return n = _n, void(); }
    void insert(int p, int r, int m) { return newRoot(), insert(roots.back(), roots[(int)roots.size() - 2], 1, n, p, r, m); }
    pll query(int ver, int l, int r) { return query(roots[ver], 1, n, l, r); }
} ST;

pair<double, int> t[maxn];
long long rsum[maxn];

class OldDriverTree {
   private:
    struct Node {
        int l, r;
        double tim;
        bool operator<(const Node& oth) const { return this->l < oth.l; }
    };

    set<Node> S;
    int n;

    void split(Node p, int v) {
        S.erase(p), S.insert({p.l, v, p.tim});
        if (v < p.r) S.insert({v + 1, p.r, p.tim});
        return;
    }

   public:
    void build(int _n, double b[]) {
        n = _n;
        for (int l = 1, r; l <= n; l = r + 1) {
            r = l;
            while (r < n && b[r + 1] == b[r]) r++;
            S.insert({l, r, b[l]});
        }
        return;
    }
    long long query(int T, int l, int r) {
        auto x = --S.lower_bound({l + 1, 0, 0});
        if (x->l != l) split(*x, l - 1);
        x = --S.lower_bound({r + 1, 0, 0});
        if (x->r != r) split(*x, r);
        long long ans = 0;
        for (auto i = S.lower_bound({l, 0, 0}); i != S.end() && i->r <= r; i = S.erase(i)) {
            double tim = T - i->tim;
            int p = lower_bound(t + 1, t + n + 1, make_pair(tim, 0)) - t;
            pll ret = ST.query(p - 1, i->l, i->r);
            ans += ret.second + (long long)((rsum[i->r] - rsum[i->l - 1] - ret.first) * tim + 0.5);
        }
        S.insert({l, r, (double)T});
        return ans;
    }
} ODT;

int s[maxn], m[maxn], r[maxn];
double b[maxn];

set<pll> S;

void solve(void) {
    int n = read<int>();
    for (int i = 1; i <= n; i++) {
        s[i] = read<int>(), m[i] = read<int>(), r[i] = read<int>();
        if (r[i])
            t[i] = {1. * m[i] / r[i], i}, b[i] = -1. * s[i] / r[i];
        else
            S.emplace(i, s[i]), t[i] = {1e18, i}, b[i] = 0;
    }
    for (int i = 1; i <= n; i++) rsum[i] = rsum[i - 1] + r[i];
    sort(t + 1, t + n + 1);
    ST.resize(n), ODT.build(n, b);
    for (int i = 1; i <= n; i++) ST.insert(t[i].second, r[t[i].second], m[t[i].second]);
    int q = read<int>();
    while (q--) {
        int t = read<int>(), l = read<int>(), r = read<int>();
        long long ans = ODT.query(t, l, r);
        for (auto i = S.lower_bound({l, 0}); i != S.end() && i->first <= r; i = S.erase(i)) ans += i->second;
        write(ans), putch('\n');
    }
    return;
}

bool mem2;

int main() {
    ios::sync_with_stdio(false);
#ifdef MACESUTED
    cerr << "Memory Cost: " << abs(&mem1 - &mem2) / 1024. / 1024. << "MB" << endl;
#endif

    int _ = 1;
    while (_--) solve();

#ifdef MACESUTED
    cerr << "Time Cost: " << clock() * 1000. / CLOCKS_PER_SEC << "MS" << endl;
#endif
    return 0;
}

Solution

考虑树为一条链时怎么做。发现若以时间为横坐标，每个人所处的在链上的位置为纵坐标，每个人可以被表示为一条线段，问题即为求线段交点横坐标最小值。在横坐标上做扫描线，维护一个 set 存放当前时刻所有出现的线段即可。相交线段在相交前一定相邻，每次插入删除时对相邻两线段求交点并于答案取较小值即可。关于 set 如何按照当前横坐标上每条线段对应的纵坐标排序，重载小于号令其按照当前时刻线段横坐标大小排序即可。虽然随扫描线推移过程原来为小于关系的两条线段不一定一直小于，但是这样打乱相对顺序的情况表示其已经出现了交点，不需要继续向后做扫描线了。因此直接按照当前时刻横坐标来比对是正确的。

至于树上情况应该怎么做，在树上进行树链剖分后，将每一个人的行动轨迹拆分到每条路径上的轻重链上即可。最终对每条轻重链执行上述操作，将所得的每条链的答案取最小值即可得到答案。

Code

View on GitHub

/**
 * @file 704E.cpp
 * @author Macesuted (i@macesuted.moe)
 * @date 2022-03-20
 *
 * @copyright Copyright (c) 2022
 * @brief
 *      My Tutorial: https://macesuted.moe/article/cf704e
 *
 */

#include <bits/stdc++.h>
using namespace std;

namespace IO {
const int SIZE = 1 << 20;
char Ibuf[SIZE], *Il = Ibuf, *Ir = Ibuf, Obuf[SIZE], *Ol = Obuf, *Or = Ol + SIZE - 1, stack[32];
char isspace(char c) { return c == ' ' || c == '\t' || c == '\n' || c == '\v' || c == '\f' || c == '\r'; }
void fill(void) { return Ir = (Il = Ibuf) + fread(Ibuf, 1, SIZE, stdin), void(); }
void flush(void) { return fwrite(Obuf, 1, Ol - Obuf, stdout), Ol = Obuf, void(); }
char buftop(void) { return Ir == Il ? fill(), *Il : *Il; }
char getch(void) { return Il == Ir ? fill(), Il == Ir ? EOF : *Il++ : *Il++; }
void putch(char x) { return *Ol++ = x, Ol == Or ? flush() : void(); }
template <typename T>
T read(void) {
    T x = 0, f = +1;
    char c = getch();
    while (c < '0' || c > '9') c == '-' ? void(f = -f) : void(), c = getch();
    while ('0' <= c && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48), c = getch();
    return x * f;
}
template <typename T>
void write(T x) {
    if (!x) putch('0');
    if (x < 0) putch('-'), x = -x;
    int top = 0;
    while (x) stack[top++] = (x % 10) ^ 48, x /= 10;
    while (top) putch(stack[--top]);
    return;
}
string getstr(const string& suf = "") {
    string s = suf;
    while (isspace(buftop())) getch();
    while (Il != Ir) {
        char* p = Il;
        while (Il < Ir && !isspace(*Il) && *Il != EOF) Il++;
        s.append(p, Il);
        if (Il < Ir) break;
        fill();
    }
    return s;
}
void putstr(string str, int begin = 0, int end = -1) {
    if (end == -1) end = str.size();
    for (int i = begin; i < end; i++) putch(str[i]);
    return;
}
struct Flusher_ {
    ~Flusher_() { flush(); }
} io_flusher_;
}  // namespace IO
using IO::getch;
using IO::getstr;
using IO::putch;
using IO::putstr;
using IO::read;
using IO::write;

bool mem1;

#define maxn 100005
#define eps 1e-10

typedef pair<int, int> pii;
typedef tuple<int, long double, int, long double> tidid;

long double TIM, ans = numeric_limits<long double>::max();

struct comp {
    long double getPos(const tidid& a) const {
        return get<1>(a) == get<3>(a) ? get<0>(a)
                                      : get<0>(a) + (TIM - get<1>(a)) * (get<2>(a) - get<0>(a)) / (get<3>(a) - get<1>(a));
    }
    bool operator()(const tidid& a, const tidid& b) const { return getPos(a) < getPos(b); }
};

vector<vector<int>> graph;
int fa[maxn], siz[maxn], son[maxn], top[maxn], dep[maxn];
vector<tidid> heav[maxn], ligh[maxn];

void dfs1(int p) {
    siz[p] = 1;
    for (auto i : graph[p])
        if (i != fa[p]) {
            fa[i] = p, dep[i] = dep[p] + 1, dfs1(i), siz[p] += siz[i];
            if (!son[p] || siz[i] > siz[son[p]]) son[p] = i;
        }
    return;
}
void dfs2(int p, int top_) {
    top[p] = top_;
    if (son[p]) dfs2(son[p], top_);
    for (auto i : graph[p])
        if (i != fa[p] && i != son[p]) dfs2(i, i);
    return;
}
int LCA(int x, int y) {
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y);
        x = fa[top[x]];
    }
    return dep[x] < dep[y] ? x : y;
}
void calcCross(tidid a, tidid b) {
    long double ak = (get<2>(a) - get<0>(a)) / (get<3>(a) - get<1>(a)), bk = (get<2>(b) - get<0>(b)) / (get<3>(b) - get<1>(b)),
                ad = get<0>(a) - get<1>(a) * ak, bd = get<0>(b) - get<1>(b) * bk;
    if ((ad < bd) != (ad + ak * TIM < bd + bk * TIM)) return;
    long double ret = (ad - bd) / (bk - ak);
    if (ret < max(get<1>(a), get<1>(b)) - eps || ret > min(get<3>(a), get<3>(b)) + eps) return;
    return ans = min(ans, ret), void();
}
void calc(vector<tidid>& a) {
    static vector<long double> pos;
    static vector<vector<tidid>> in, out;
    pos.clear(), pos.reserve(2 * a.size()), in.clear(), out.clear();
    for (auto i : a) pos.push_back(get<1>(i)), pos.push_back(get<3>(i));
    sort(pos.begin(), pos.end()), pos.resize(unique(pos.begin(), pos.end()) - pos.begin());
    in.resize(pos.size()), out.resize(pos.size());
    for (auto i : a)
        in[lower_bound(pos.begin(), pos.end(), get<1>(i)) - pos.begin()].push_back(i),
            out[lower_bound(pos.begin(), pos.end(), get<3>(i)) - pos.begin()].push_back(i);
    static set<tidid, comp> S1;
    S1.clear();
    for (int i = 0; i < (int)pos.size(); i++) {
        TIM = pos[i];
        if (TIM > ans) return;
        for (auto j : in[i]) {
            auto ret = S1.emplace(j);
            if (!ret.second) return ans = min(ans, pos[i]), void();
            auto pl = ret.first, pr = pl;
            if (pl != S1.begin()) calcCross(*--pl, j);
            if (++pr != S1.end()) calcCross(j, *pr);
        }
        for (auto j : out[i]) {
            auto p2 = S1.erase(S1.find(j)), p1 = p2;
            if (p1 != S1.begin() && p2 != S1.end()) calcCross(*--p1, *p2);
        }
    }
    return;
}

void solve(void) {
    int n = read<int>(), m = read<int>();
    graph.resize(n + 1);
    for (int i = 1; i < n; i++) {
        int x = read<int>(), y = read<int>();
        graph[x].push_back(y), graph[y].push_back(x);
    }
    dfs1(1), dfs2(1, 1);
    for (int i = 1; i <= m; i++) {
        long double tim = read<int>(), c = read<int>();
        int x = read<int>(), y = read<int>(), t = LCA(x, y);
        while (top[x] != top[t]) {
            heav[top[x]].emplace_back(x, tim, top[x], tim + (dep[x] - dep[top[x]]) / c), tim += (dep[x] - dep[top[x]]) / c,
                x = top[x];
            ligh[x].emplace_back(x, tim, fa[x], tim + 1 / c), tim += 1 / c, x = fa[x];
        }
        static stack<pii> cache;
        while (!cache.empty()) cache.pop();
        while (top[y] != top[t]) cache.emplace(y, top[y]), y = fa[top[y]];
        heav[top[y]].emplace_back(x, tim, y, tim + abs(dep[x] - dep[y]) / c), tim += abs(dep[x] - dep[y]) / c;
        while (!cache.empty()) {
            pii p = cache.top();
            cache.pop();
            ligh[p.second].emplace_back(fa[p.second], tim, p.second, tim + 1 / c), tim += 1 / c;
            heav[p.second].emplace_back(p.second, tim, p.first, tim + (dep[p.first] - dep[p.second]) / c),
                tim += (dep[p.first] - dep[p.second]) / c;
        }
    }
    for (int i = 1; i <= n; i++) {
        for (auto& j : heav[i]) get<0>(j) = dep[get<0>(j)] - dep[i] + 1, get<2>(j) = dep[get<2>(j)] - dep[i] + 1;
        for (auto& j : ligh[i]) get<0>(j) = dep[get<0>(j)] - dep[i] + 2, get<2>(j) = dep[get<2>(j)] - dep[i] + 2;
        calc(heav[i]), calc(ligh[i]);
    }
    if (ans == numeric_limits<long double>::max()) return putstr("-1\n");
    cout << setiosflags(ios::fixed) << setprecision(30) << ans << endl;
    return;
}

bool mem2;

int main() {
    ios::sync_with_stdio(false);
#ifdef MACESUTED
    cerr << "Memory Cost: " << abs(&mem1 - &mem2) / 1024. / 1024. << "MB" << endl;
#endif

    int _ = 1;
    while (_--) solve();

#ifdef MACESUTED
    cerr << "Time Cost: " << clock() * 1000. / CLOCKS_PER_SEC << "MS" << endl;
#endif
    return 0;
}