该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

Description

最近，小 E 学习了一种叫做并查集的数据结构。这种强大的数据结构可以维护一张图，支持向图中加入一条无向边，查询两点是否连通。

具体来说，并查集的结构是一个由 $n$ 个点构成的有根树森林，每个节点 $x$ 有父亲 $f[x]$。如果 $x = f[x]$，这意味着 $x$ 恰好就是其所在有根树的根节点。初始时，每个节点单独构成一个有根树，即对于所有 $1 \leq x \leq n$，有 $x = f[x]$。

一个标准的并查集包含以下两种基本操作：

• $\text{find} \ x$：返回 $x$ 所在有根树的根。
• $\text{unite} \ x \ y$：令 $x' \gets \text{find}(x)$，$y' \gets \text{find}(y)$。然后若 $x'=y'$，那么我们什么都不做，否则令 $f[x'] \gets y$。

为了加速 $\text{unite}$ 操作，小 E 使用了路径压缩。即，如果我们对于节点 $x$ 调用了函数 $\text{find}(x)$，那么对于 $x$ 到根 $r$ 的路径上的所有节点 $v$，执行 $f[v] \gets r$。

为了帮助选手更好地理解题意，这里给出了一份更为详细的，用伪代码实现的路径压缩并查集：

小 E 十分喜欢并查集，因此他想要做一些更深刻的研究。他生成了一个长度为 $n$ 的序列 $f$ 表示每个节点的父亲，初始时对所有 $1 \leq i \leq n$ 满足 $f[i] = i$。然后，小 E 会进行若干次（可能为 $0$ 次）操作，每次操作为以下两种之一：

• 选择一个整数 $1 \leq x \leq n$，执行 $\text{find}(x)$。
• 选择两个整数 $1 \leq x,y \leq n$，执行 $\text{unite}(x,y)$。

小 E 将所有操作之后的 $f$ 数组告诉了你。但今夜你不关心小 E，你只想知道对于给定的另一个数组 $g$，你是否能够通过对 $f$ 做以上给出的两种操作，使得对于任意 $1 \leq i \leq n$，都有 $f[i] = g[i]$。

为了检验你是否真的懂，你需要构造出一个满足条件的操作序列，或报告无解。

温馨提示：你可以在 【输出格式】 中得到有关于构造方式的更多信息。

Format

Input

第一行一个正整数 $T$，表示数据组数。

接下来一共 $T$ 组数据，在每组数据中：

第一行一个正整数 $n$，表示小 E 所生成的序列的长度。

第二行 $n$ 个正整数 $f_1,f_2,\cdots,f_n$，描述小 E 给你的序列，这也是你的初始序列。

第三行 $n$ 个正整数 $g_1,g_2,\cdots,g_n$，描述目标序列。

Output

对于每一组数据，如果不存在合法的操作方案，则输出一行一个整数 $\texttt{-1}$。

否则，输出的第一行应当仅包含一个整数 $m$，表示你的方案所用的操作次数。你需要保证 $\bm{0 \leq m \leq 2 \times n^2}$。

接下来 $m$ 行，每行包含两个或三个正整数，整数之间用一个空格隔开。

若为两个整数 $\texttt{1 x}$，则表示进行一次 $\text{find}(x)$ 操作。

若为三个整数 $\texttt{2 y z}$，则表示进行一次 $\text{unite}(y,z)$ 操作。

你需要保证 $1 \leq x,y,z \leq n$，且 $y \neq z$。

Samples

5
3
1 2 3
2 2 3
4
1 2 3 3
1 1 1 2
5
1 2 3 4 5
2 3 4 5 5
5
1 1 1 1 1
1 2 3 4 5
6
1 2 2 4 5 6
1 1 5 1 4 2

1
2 1 2
4
2 3 2
1 4
2 2 1
1 3
4
2 1 2
2 1 3
2 2 4
2 3 5
-1
7
2 6 2
2 2 5
1 3
2 2 4
1 2
2 2 1
1 2

见附件中的 dsu/dsu2.in。

见附件中的 dsu/dsu2.ans。

见附件中的 dsu/dsu3.in。

见附件中的 dsu/dsu3.ans。

Limitation

【样例解释 #1】

对于第二组测试数据，下图是初始状态，其中没有出边的点代表一个自环。

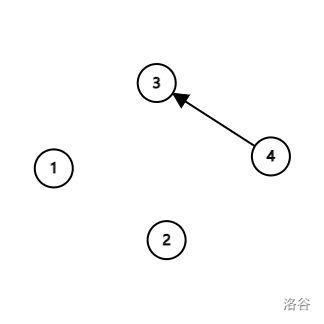
下图是第一次操作之后的结果。

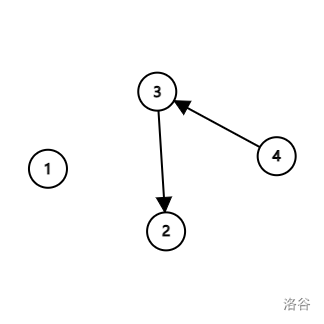
下图是第二次操作之后的结果。

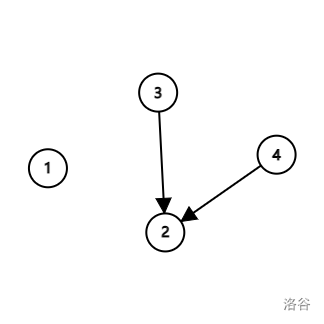
下图是第三次操作之后的结果。

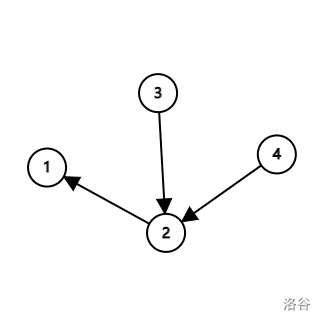
下图是第四次操作之后的结果。

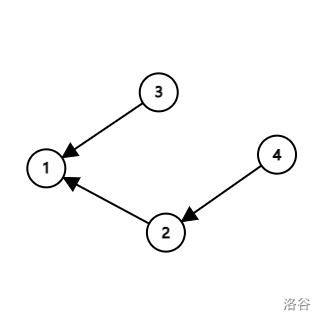
【样例解释 #2】

该样例满足测试点 $8 \sim 11$ 的条件限制。

【样例解释 #3】

该样例满足测试点 $12 \sim 15$ 的条件限制。

【数据范围】

设 $\sum n^2$ 为所有 $T$ 组数据中 $n^2$ 的总和。

对于所有数据，保证 $\sum n^2 \leq 5 \times 10^6$，$3 \leq n \leq 1000$，$1 \leq f_i,g_i \leq n$。

【评分方式】

对于每一组数据，若你的输出格式正确，且在按顺序进行所有操作后，对于所有 $1 \leq i \leq n$ 都有 $f[i] = g[i]$，则认为你的答案正确。

【提示】

你的输出不需要与样例输出一致，输出任意一个合法解即可得分。

【校验器】

为了方便选手测试，在附件中的 $\texttt{dsu}$ 目录下我们下发了 $\texttt{checker.cpp}$ 文件，选手可以编译该程序，并使用它校验自己的输出文件。但请注意它与最终评测时所使用的校验器并不完全一致。你也不需要关心其代码的具体内容。

编译命令为：g++ checker.cpp -o checker -std=c++14。

$\texttt{checker}$ 的使用方式为：checker <inputfile> <outputfile> <answerfile>，参数依次表示输入文件、你的输出文件及答案文件。请保证文件 $\texttt{testlib.h}$、$\texttt{checker.cpp}$、输入文件、你的输出文件及答案文件均在同一子目录下。

若该组数据无解，但你给出了一组方案，则校验器会给出错误信息 too young.。若该组数据有解，但你输出了 $\texttt{-1}$，则校验器会给出错误信息 too simple.。

若你给出的操作数超过了 $2 \times n^2$，校验器会给出错误信息 too many operations.。否则，若你输出的数字大小范围不合法，则校验器会给出错误信息 invalid output.。

若你的输出数字大小范围正确，但方案错误，则校验器会给出错误信息 wrong answer.。

若你的方案正确，校验器会给出 OK。