#P6776. [NOI2020] 超现实树
[NOI2020] 超现实树
题目背景
下课铃声响起,机房里的两位女生从座位上站起来。(下面用 , 代指两人)
:省选前的集训真难熬啊…… 听课、考试、讲评、补题 —— 对于现在的我来说,即使在梦里想到一道数据结构题,也会不由自主地开始思考吧。
:重复训练对我来说似乎并不是什么负担,但我确实感觉到解决题目带来的愉悦感在最近逐渐减弱了。也许我们需要一些精神上的 “刺激”:一些不拘泥于繁复技术的智力游戏,来让我们找回对于数学和算法的兴趣。
:咦,我好像收到了一封用英文写的短信,似乎是…… 数学书上的一些片段。
题目描述
:我来翻译一下短信的内容。
定义:本文所述的树是归纳定义的:单独的结点构成一棵树,以一棵树作为左(或右)孩子可以构成一棵树,以两棵树分别作为左、右孩子也可以构成一棵树。仅由以上规则用有限步生成的所有结构被称为树。
:也就是说,这里所说的树是指非空、有根、区分左右孩子的二叉树。
:的确如此。接下来书上定义了两棵树的同构。
定义:称两棵树 , 同构,记做 ,由以下四条规则定义:
- 由单独结点构成的树是彼此同构的;
- 如果两棵树的根结点均只有左子树,并且它们的左子树同构,那么这两棵树是同构的;
- 如果两棵树的根结点均只有右子树,并且它们的右子树同构,那么这两棵树是同构的;
- 如果两棵树的根结点均有左、右子树,并且它们的左、右子树分别对应同构,那么这两棵树是同构的。
很明显,同构关系构成了所有树上的一个等价关系。为了方便,我们将同构的树看作相同的树。
:将同构的树看成相同的树就是说树的结点是彼此相同的。简单地说,两棵树同构当且仅当他们在结点无标号、区分左右孩子的意义下相同;我们说两棵树不同,当且仅当它们不同构。
:书里还定义了树的叶子:和通常的定义一样,叶子指没有任何孩子的结点。
:这和我们熟悉的定义完全一致。嘛,数学家真是有点啰嗦…… 恐怕只有 那种家伙会喜欢这种做派吧。
:我倒是对此不太反感 —— 比起基于经验的 “直觉”,准确的定义和严谨的证明还是更加让人安心。你看,下一个定义就没有那么直观了。
定义:称一棵树 单步替换成为 ,如果将 的某一叶子结点替换为另一棵树 得到的树与 同构,记做 ;称一棵树 替换成为 ,记做 ,如果存在自然数 和树 ,使得 $T \equiv T_{1} \rightarrow T_{2} \rightarrow \cdots \rightarrow T_{n} \equiv T^{\prime}$。
:我来想想…… 所谓替换,就是删掉某个叶子结点并在对应的位置放入另一棵树,就像那个叶子结点 “长出了” 一个更大的子树一样;一棵树替换成为另一棵树,说明它可以经由零次、一次或多次单步替换得到那棵树。哦…… 我明白了!举例来说,任何一棵树都可以替换成它本身,换言之对于树 ,都有 。下面这个图片可以帮助理解单步替换和替换的含义。

:你说得对。特别地,任何一棵树都可以替换得到无穷多棵不同的树,并且仅有一个结点构成的树可以替换得到任意其他的树。书上也有定义这样的东西。
定义:对于一棵树 ,定义 表示 T 所能替换构成的树的集合,即 $\operatorname{grow}(T)=\left\{T^{\prime} \mid T \rightarrow^{\star} T^{\prime}\right\}$。更近一步,如果 $\mathscr{T}=\left\{T_{1}, T_{2}, \ldots, T_{n}\right\}$ 是一个树的有限集合,定义 为所有 的并集,其中 。即
$$\operatorname{grow}(\mathscr{T})=\bigcup_{T_{i} \in \mathscr{T}} \operatorname{grow}\left(T_{i}\right) $$
:我们把 称作树的集合 所生长得到的集合吧 —— 也就是说,树的集合 所生长得到的集合包含所有可以被某个 替换得到的树。不妨把树的集合叫做树林。不太严谨地说,一个树林所生长得到的新树林就是其中所有树、以所有可能的方式生长得到的树林。显而易见,一个非空树林所生长得到的树林都是无穷树林。但这个无穷树林,或者说 ,并不一定包含所有的树 —— 更进一步,它甚至不一定包含 “几乎所有” 的树。
:让我来补充一下:我们称一个树林是几乎完备的(或称几乎包含了所有的树),如果仅有有限多的树不在其中。对于一个有限树林 , 要么包含了所有的树,要么包含了几乎所有的树,要么存在无穷多棵树不在其中。如果这是一道 OI 题,出题人一定会在样例中给出三种情况的例子吧。书上的关键定理也用了和我们相同的定义。
定理(几乎完备的可判定性):一个树的集合是几乎完备的,如果仅有有限棵树不在其中。那么,对于一个给定的树的有限集合 ,存在高效的算法判定 是否是几乎完备的。
:这个问题变成一个纯粹的 OI 题目了!让我用我们的语言来重述一下题意:给定一个有限大小的树林 ,判定 是否是几乎完备的,即是否仅有有限棵树不能被树林中所包含的树生长得到。
:也就是说,给定一个有限的树的集合 ,判定是否仅有有限个树 ,满足 。所谓 ,就是说不存在 ,使得 。这和通常的 OI 题目的确非常不同:我甚至没有想到这个问题的一个算法。
:我也一样,不过我很久没有感受到这种解决未知问题的冲动了。
输入格式
本题有多组测试数据,输入文件的第一行包含一个正整数 ,表示测试数据的组数。接下来包含恰好 组测试数据,每组测试数据具有以下的格式:
第一行是一个正整数 ,表示树的集合中树的个数。接下来按照以下格式输入 棵树:
- 首先是一个正整数 ,表示树中的结点个数,结点编号为 ;
- 接下来 行每行两个非负整数,其中第 行从左到右包含用空格隔开的 和 ,分别表示 号结点左、右孩子结点的编号。如果左(或右)孩子不存在,那么 (或 )为 。当然,叶结点一定满足 。
- 输入数据保证构成一棵以 号结点作为根结点的树。请注意:结点的编号只是为了方便输入,任何同构的树都被视为是相同的。
所输入的 棵树中可能存在彼此同构的树;如果去除这些重复的树(即每种同构的树只留下一个),它们可以构成一个树的集合 。你需要判定这一树的集合所生长得到的集合 是否是几乎完备的。
输出格式
输出包含 行,分别表示 组测试数据的答案。其中,第 行输出一个字符串:如果第 组测试数据所输入的树的集合所生长得到的集合是几乎完备的(换言之,仅有有限棵树不能被其生长得到),那么输出 Almost Complete;否则输出 No。请注意输出字符串的拼写和大小写。
1
1
1
0 0
Almost Complete
1
3
3
2 3
0 0
0 0
2
2 0
0 0
2
0 2
0 0
Almost Complete
1
2
3
2 3
0 0
0 0
2
2 0
0 0
No
提示
样例 2 解释
这一样例仅包含一组测试数据,其中树的集合 包含三棵树,如下图所示。容易发现,仅有单个结点构成的树不在 中,其包含了几乎所有树,因而是几乎完备的。
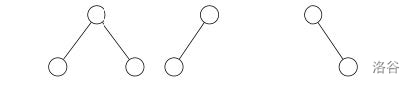
样例 3 解释
这一样例仅包含一组测试数据,其中树的集合 包含两棵树。容易发现,对于所有的 ,包含 个结点,每个非叶结点仅有右孩子的链状树都不在 中,因而存在无穷多棵树不在 中, 不是几乎完备的。
样例 4
见选手目录下的 surreal/surreal4.in 与 surreal/surreal4.ans。
测试点约束
全部数据满足:, , , 。其中, 表示这一测试点所有测试数据中所出现的所有树的结点个数之和; 表示这一测试点中所有测试数据中所出现的树的个数; 表示这一测试点中所出现的所有树的最高高度(仅包含一个结点的树高度为 )。下表中的表项 , 和 含义与上面相同,描述了每一组测试点的数据范围。
特殊性质:下面是下表中会涉及的四种特殊性质的解释。
- 特殊性质 :对于这一测试点中的每一组测试数据,都有 ,即树的集合中包括不超过 棵树;
- 特殊性质 :对于这一测试点中的每一组测试数据,树的集合中所有的树具有相同的高度;
- 特殊性质 :对于这一测试点中的每一组测试数据,树的集合仅包含链(换言之,每个非叶结点仅包含一个孩子);
- 特殊性质 :对于这一测试点中的每一组测试数据,树的集合仅包含满足以下两个条件之一的树:
- 每个非叶结点仅包含一个孩子;
- 恰好有两个叶结点,它们具有相同的父结点,并且除这三个结点外,其余结点均有且仅有一个孩子。
每个测试点的具体限制见下表:
| 测试点编号 | 特殊性质 | ||||
|---|---|---|---|---|---|
| 无 | |||||
| 性质 | |||||
| 无 | |||||
| 性质 | |||||
| 无 | |||||
| 性质 | |||||
| 无 | |||||
| 性质 | |||||
| 性质 | |||||
| 无 | |||||
