题目背景

滚粗了的 HansBug 在收拾旧语文书，然而他发现了什么奇妙的东西。

题目描述

蒟蒻 HansBug 在一本语文书里面发现了一本答案，然而他却明明记得这书应该还包含一份练习题。然而出现在他眼前的书多得数不胜数，其中有书，有答案，有练习册。已知一个完整的书册均应该包含且仅包含一本书、一本练习册和一份答案，然而现在全都乱做了一团。许多书上面的字迹都已经模糊了，然而 HansBug 还是可以大致判断这是一本书还是练习册或答案，并且能够大致知道一本书和答案以及一本书和练习册的对应关系（即仅仅知道某书和某答案、某书和某练习册有可能相对应，除此以外的均不可能对应）。既然如此，HansBug 想知道在这样的情况下，最多可能同时组合成多少个完整的书册。

输入格式

第一行包含三个正整数 $N_1$、$N_2$、$N_3$，分别表示书的个数、练习册的个数和答案的个数。

第二行包含一个正整数 $M_1$，表示书和练习册可能的对应关系个数。

接下来 $M_1$ 行每行包含两个正整数 $x$、$y$，表示第 $x$ 本书和第 $y$ 本练习册可能对应。（$1$$\leq$$x$$\leq$$N_1$，$1$$\leq$$y$$\leq$$N_2$）

第 $M_{1+3}$ 行包含一个正整数 $M_2$，表述书和答案可能的对应关系个数。

接下来 $M_2$ 行每行包含两个正整数 $x$、$y$，表示第 $x$ 本书和第 $y$ 本答案可能对应。（$1$$\leq$$x$$\leq$$N_1$，$1$$\leq$$y$$\leq$$N_3$）

输出格式

输出包含一个正整数，表示最多可能组成完整书册的数目。

5 3 4
5
4 3
2 2
5 2
5 1
5 3
5
1 3
3 1
2 2
3 3
4 3

2

提示

样例说明：

如题，$N_1=5$，$N_2=3$，$N_3=4$，表示书有 $5$ 本、练习册有 $3$ 本、答案有 $4$ 本。

$M_1=5$，表示书和练习册共有 $5$ 个可能的对应关系，分别为：书 4 和练习册 3、书 2 和练习册 2、书 5 和练习册 2、书 5 和练习册 1 以及书 5 和练习册 3。

$M_2=5$，表示数和答案共有 $5$ 个可能的对应关系，分别为：书 1 和答案 3、书 3 和答案 1、书 2 和答案 2、书 3 和答案 3 以及书 4 和答案 3。

所以，以上情况的话最多可以同时配成两个书册，分别为：书 2 + 练习册 2 + 答案 2、书 4 + 练习册 3 + 答案 3。

数据规模：

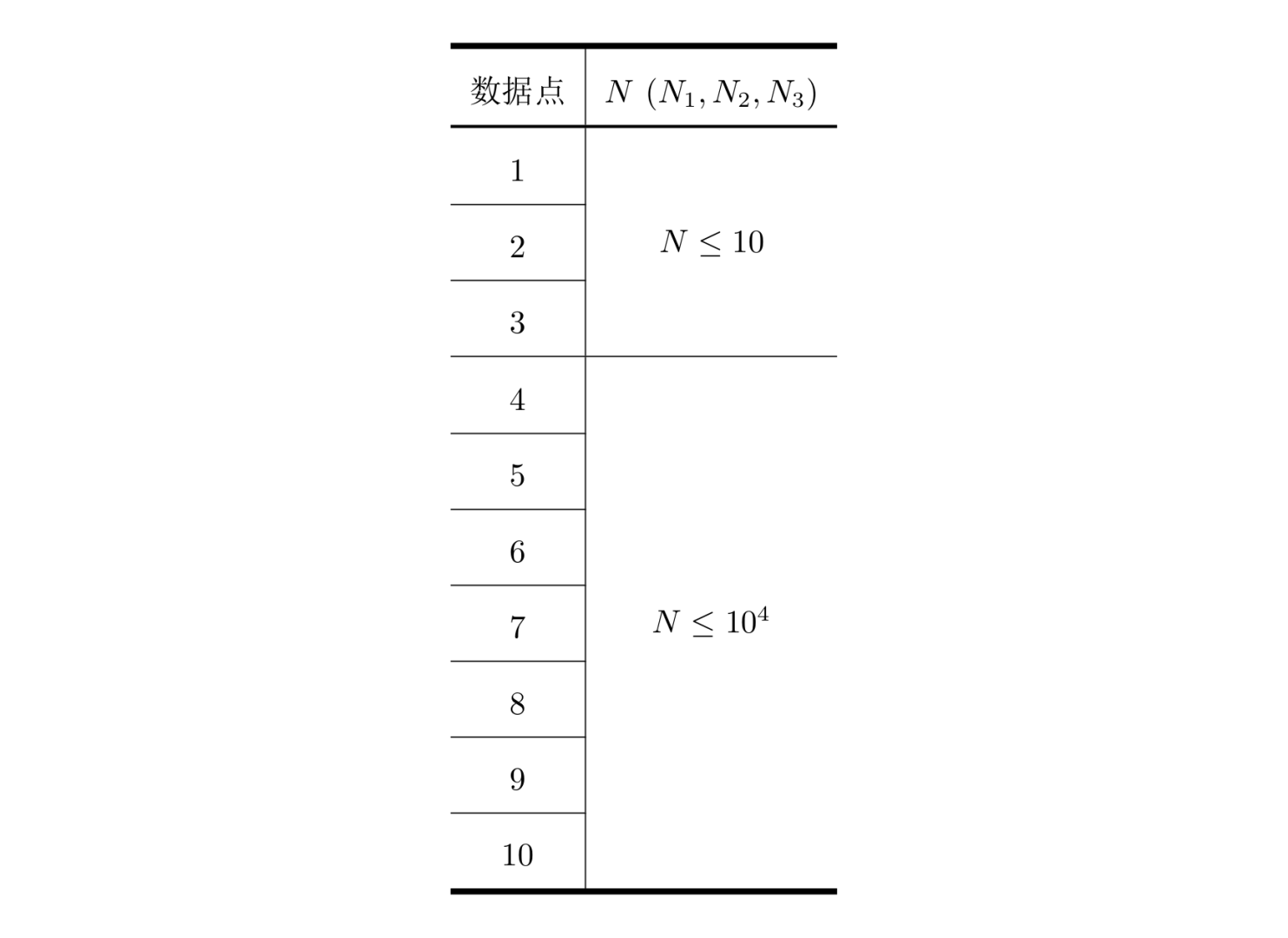
对于数据点 $1$, $2$, $3$，$M_1$, $M_2\leq 20$

对于数据点 $4-10$，$M_1$, $M_2 \leq 20000$