#HTR002B. 丑国传说 · 寻找丑星
丑国传说 · 寻找丑星
本题复杂度假了。
题目背景
bh 摆脱了语文作业的统治,和 ac 以及 mc 躺在楼顶上看星星。他们想在星空中找到丑星系。
题目描述
bh 在星空中看到了 颗星星,第 颗星星位于 。
ac 告诉 bh,丑星系由 颗丑星依次排列而成,每颗丑星都对应了星空中的一颗星星。但是 ac 忘了丑星系的具体位置,只记得丑星系相邻两颗丑星的相对位置。
规定:
- 相邻:对于 ,丑星 与丑星 相邻;丑星 与丑星 相邻。
- 相对位置:对于丑星系中的相邻的两颗丑星 和 ,如果 在 的 方向,那么相应的,在星空中, 对应的星星也一定在 对应的星星的 方向,但在距离上没有限制。
现在 ac 以坐标的形式给出 组相对位置,bh 能否在星空中找到丑星系对应的星星?
简化版题意:
给定 个点,第 个点的坐标为 ,还有另外 个点,第 个点的坐标为 ,问是否存在一个长度为 的数列 满足:
- 且互不相同。
- ,存在 满足 ,。
特殊地,令 $a_{n+1}=a_1,\,b_{n+1}=b_1,\,x_{c_{n+1}}=x_{c_{1}},\,y_{c_{n+1}}=y_{c_1}$。
输入
第一行一个正整数数 ,表示 bh 看到的星星个数。
从第二行开始 行,每行两个整数 ,表示 bh 看到的第 颗星星在天空中的位置。
第 行一个正整数 ,表示丑星系的丑星个数。
第 行开始 行,每行两个整数 ,表示 组相对位置。
输出
第一行一个字符串,如果能看到,输出 Yes ,否则输出 No。
如果能看到,再输出 个整数,表示组成丑星系的各星对应天空中星星的编号。如果有多个结果,那么输出编号字典序最小的。
每行最多输出 个数字。每 个数字换一行。
8
0 0
1 1
0 3
1 2
1 3
2 3
2 4
1 5
4
0 0
2 2
2 4
0 6
Yes
1 2 4 3
6
1 1
0 0
-1 1
0 2
2 0
1 -1
4
1 1
2 2
3 1
2 0
Yes
2 1 5 6
10
1 2
2 45
35 43
3 43
-135 -57
-53 57
-65 77
434 -87
-67 68
-4 53
2
1 32
3 7
No
样例二解释:
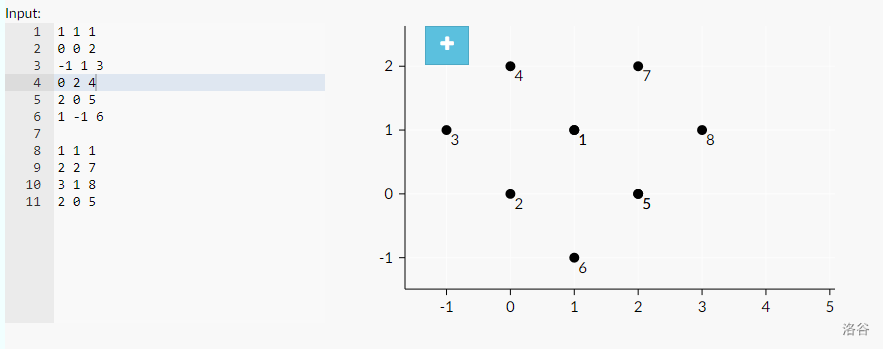
如图所示, 为星星在天空中的位置, 为丑星系的位置。满足条件的组合有 和 。相比之下后者的字典序更小。
数据范围
对于 的数据,。
对于 的数据,,。
保证答案中存在 No。
