#P2492. [SDOI2011] 火星移民
[SDOI2011] 火星移民
题目描述
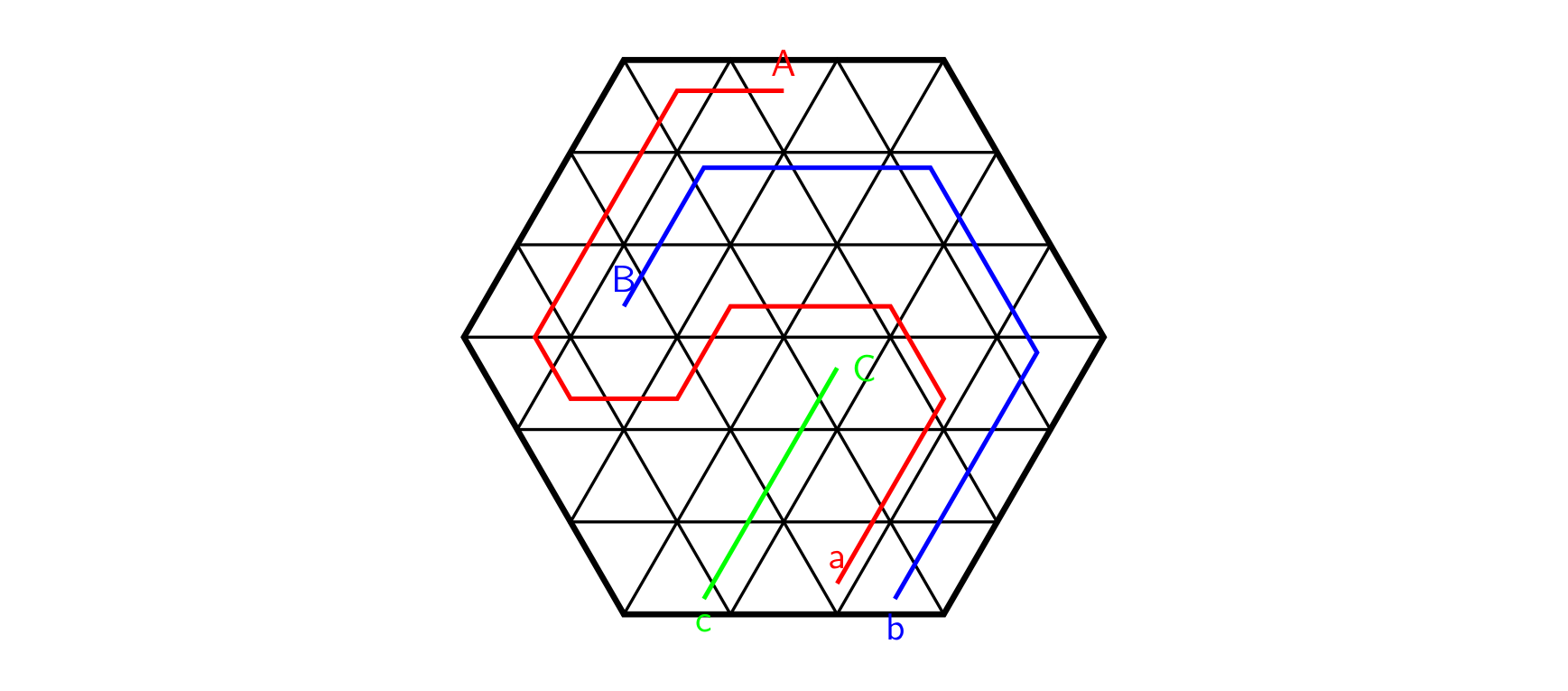
在 2xyz 年,人类已经移民到了火星上。由于工业的需要,人们开始在火星上采矿。火星的矿区是一个边长为 的正六边形,为了方便规划,整个矿区被分为 个正三角形的区域(如图 )。

整个矿区中存在 矿, 矿, 矿三个矿场,和 厂, 厂, 厂三个炼矿厂。每个三角形的区域可以是一个矿场、炼矿厂、山地、或者平地。
现在矿区管理局要求建立一个交通系统,使得矿场和对应炼矿厂之间存在一条公路,并且三条公路互不交叉(即一个三角形区域中不存在两条以上运输不同矿的公路)。两个三角形区域是相邻的当且仅当这两个三角形存在公共边,只有相邻的两个区域之间才能建一段路,建这段路的费用为 。
注意,山地上是不能建公路的。由于火星金融危机的影响,矿区管理局想知道建立这样一个交通系统最少要花多少费用。更多的,当局向知道有多少种花费最小的方案。
输入格式
第 行一个整数 。表示这个矿区是边长为 的正六边形。
接下来有 的整数,分为 行,表示矿区当前区域的情况。 表示平地, 表示对应的矿区或者炼矿厂, 表示山地。(样例 对应图 )。
可能有多组数据,请处理到文件结尾。
输出格式
对于每组数据,包含两个整数,表示最小费用和达到最小费用的方案数。如果找不到符合要求的方案,输出 。由于方案数可能过大,所以请把方案数 。
2
0 1 0 0 0
0 0 2 0 4 0 0
0 0 4 3 0 3 2
0 0 0 1 0
18
3
0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0
0 0 2 0 0 0 0 0 0 0 0
0 0 0 0 0 0 3 0 0 0 0
0 0 0 0 0 0 0 0 0
0 3 0 1 0 2 0
44
提示
样例2解释
【数据规模和约定】
对于 的数据,。
对于 的数据,。
