#P2047. [NOI2007] 社交网络
[NOI2007] 社交网络
题目描述
在社交网络 ( Social Network ) 的研究中,我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题:
在一个社交圈子里有 个人,人与人之间有不同程度的关系。我们将这个关系网络对应到一个 个结点的无向图上,两个不同的人若互相认识,则在他们对应的结点之间连接一条无向边,并附上一个正数权值 , 越小,表示两个人之间的关系越密切。我们可以用对应结点之间的最短路长度来衡量两个人 和 之间的关系密切程度,注意到最短路径上的其他结点为 和 的联系提供了某种便利,即这些结点对于 和 之间的联系有一定的重要程度。我们可以通过统计经过一个结点 的最短路径的数目来衡量该结点在社交网络中的重要程度。考虑到两个结点 和 之间可能会有多条最短路径。我们修改重要程度的定义如下:令 表示从s到t的不同的最短路的数目, 表示经过 从 到 的最短路的数目;则定义:
为结点 在社交网络中的重要程度。为了使 和 有意义,我们规定需要处理的社交网络都是连通的无向图,即任意两个结点之间都有一条有限长度的最短路径。现在给出这样一幅描述社交网络的加权无向图,请你求出每一个结点的重要程度。
输入格式
输入第一行有两个整数 和 ,表示社交网络中结点和无向边的数目。
在无向图中,我们将所有结点从 到 进行编号。
接下来 行,每行用三个整数 描述一条连接结点 和 ,权值为 的无向边。 注意任意两个结点之间最多有一条无向边相连,无向图中也不会出现自环(即不存在一条无向边的两个端点是相同的结点)。
输出格式
输出包括 行,每行一个实数,精确到小数点后 位。第 行的实数表示结点 在社交网络中的重要程度。
4 4
1 2 1
2 3 1
3 4 1
4 1 1
1.000
1.000
1.000
1.000
提示
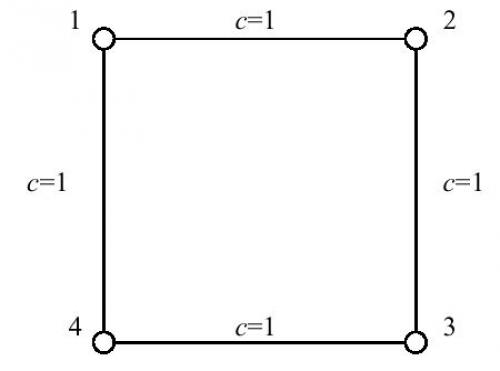
对于1号结点而言,只有2号到4号结点和4号到2号结点的最短路经过1号结点,而2号结点和4号结点之间的最短路又有2条。因而根据定义,1号结点的重要程度计算为1/2+1/2=1。由于图的对称性,其他三个结点的重要程度也都是1。
对于 的数据, 。
对于 的数据, ,任意一条边的权值 是正整数且 。
所有数据中保证给出的无向图连通,且任意两个结点之间的最短路径数目不超过 。
