#P1301. 魔鬼之城
魔鬼之城
题目描述
在一个被分割为 个正方形房间的矩形魔鬼之城中,一个探险者必须遵循下列规则才能跳跃行动。他必须从 进入,从 走出;在每一房间的墙壁上都写了一个魔法数字,是 之内的自然数;探险者可以想像出 个方向中的任何一个(水平或垂直或对角线方向),随后他就可以作一次空间跳跃穿过这一方向上的连续的 个房间,其中 是他原来所在房间的魔法数字。但如果在这一方向上的房间数小于 ,则他不作任何跳跃,而必须想像另一个方向。同时,探险者不能作连续两次相同方向的跳跃。
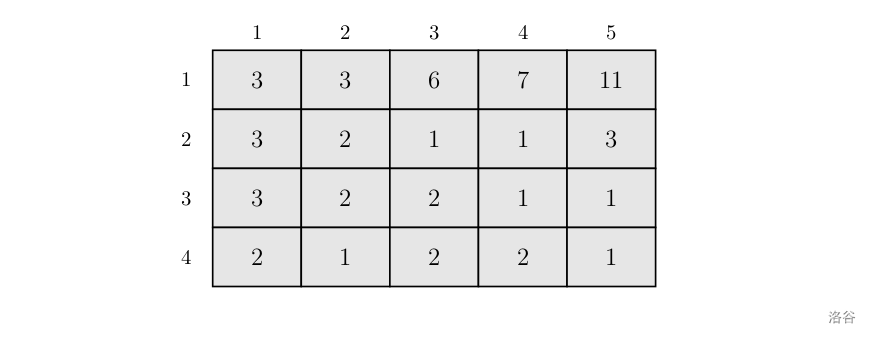
例如在上图的 的魔鬼之城中,如果探险者现在所在的位置是 ,那么通过依次空间跳跃他可以到达下列房间中的一个:,,,,或 。另外,如果他要用两次跳跃从 到达 ,则他不能首先跳到 (因为这样他第二次跳跃的方向将和第一次相同,而这是不允许的)。所以他必须先跳跃到 。 请你写一个程序,对给定的地图,算出探险者至少需要跳跃多少步才能离开魔鬼之城。
输入格式
第一行两个整数 。
下来有 行,每行为 个自然数,表示对应房间中的魔法数字。
输出格式
出最小步数,如果探险者无法离开魔鬼之城,请输出 NEVER。
5 4
3 3 6 7 11
3 2 1 1 3
3 2 2 1 1
2 1 2 2 1
4
