题目描述
猪小侠最近学习了最长上升子序列的相关知识。对于一个整数序列 A=(a1,a2,…,ak),定义 A 的子序列为:从 A 中删除若干个元素后(允许不删,也允许将所有 k 个元素都删除),剩下的元素按照原来的顺序所组成的序列。如果这个子序列的元素从左到右严格递增,则称它为 A 的一个上升子序列。其中包含元素数量最多的上升子序列称为 A 的最长上升子序列。例如,(2,4,5,6) 和 (1,4,5,6) 都是 (2,1,1,4,7,5,6) 的最长上升子序列,长度都为 4。
现在猪小侠遇到了这样一个问题:给定一个序列 Bm=(b1,b2,…,bm),设 C 是 Bm 的子序列,且 C 的最长上升子序列的长度不超过 k,则 C 的长度最大能是多少?
猪小侠觉得这个问题太简单了,缺乏挑战,他决定提出一个更难的问题。于是他给了你这样一个序列 B=(b1,b2,…,bn),以及若干次询问。每次询问会给定两个整数 m 和 k,你需要对于 B 序列的前 m 个元素构成的序列 Bm=(b1,b2,…,bm) 和 k 回答上述问题。
输入格式
第一行两个整数 n,q,其中 n 是序列 B 的长度,q 是询问次数。
第二行是空格隔开的 n 个正整数 b1,b2,…,bn。
接下来 q 行,其中第 i 行包含两个整数 mi,ki,表示对 m=mi,k=ki 进行询问。
输出格式
输出共 q 行,按顺序每行一个整数作为回答。
11 6
9 6 3 1 5 12 8 4 2 2 2
5 1
7 2
9 1
9 2
11 1
11 11
4
6
5
8
7
11
提示
【样例解释】
询问 1:对于序列 (9,6,3,1,5),可以选取子序列 (9,6,3,1),它的最长上升子序列长度为 1。
询问 2:对于序列 (9,6,3,1,5,12,8),可以选取子序列 (9,6,3,1,12,8),它的最长上升子序列长度为 2。
询问 3:对于序列 (9,6,3,1,5,12,8,4,2),可以选取子序列 (9,6,5,4,2),它的最长上升子序列长度为 1。
询问 4:对于序列 (9,6,3,1,5,12,8,4,2),可以选取子序列 (9,6,3,1,12,8,4,2),它的最长上升子序列长度为 2。
询问 5:对于序列 (9,6,3,1,5,12,8,4,2,2,2),可以选取子序列 (9,6,5,4,2,2,2),它的最长上升子序列长度为 1。
询问 6:对于序列 (9,6,3,1,5,12,8,4,2,2,2),可以选取子序列 (9,6,3,1,5,12,8,4,2,2,2),它的最长上升子序列长度为 3。
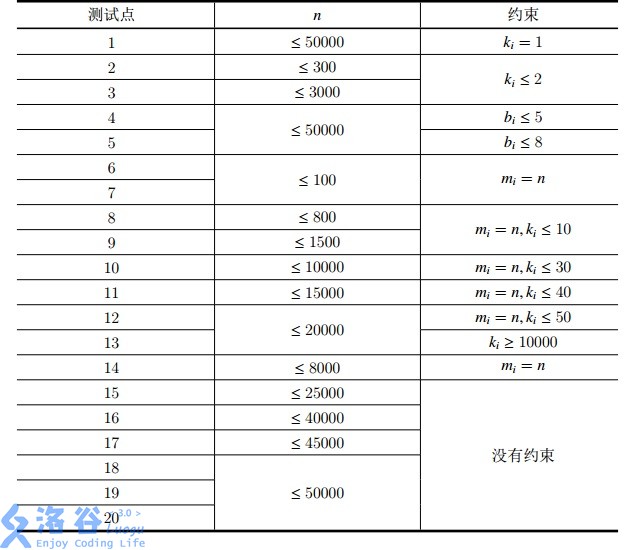
对于 100% 的数据, 1≤n≤5×104,1≤bi≤5×104,1≤q≤2×105,1≤ki≤mi≤n。

