题目描述
一条狭长的纸带被均匀划分出了 n 个格子,格子编号从 1 到 n 。每个格子上都染了一种颜色 colori 用 [1,m] 当中的一个整数表示),并且写了一个数字 numberi 。
定义一种特殊的三元组:(x,y,z) ,其中 x,y,z 都代表纸带上格子的编号,这里的三元组要求满足以下两个条件:
-
x , y , z是整数, x < y < z , y−x=z−y 。
-
colorx=colorz
满足上述条件的三元组的分数规定为 (x+z) × (numberx+numberz) 。整个纸带的分数规定为所有满足条件的三元组的分数的和。这个分数可能会很大,你只要输出整个纸带的分数除以 10,007 所得的余数即可。
输入格式
第一行是用一个空格隔开的两个正整数 n 和 m , n 表纸带上格子的个数, m 表纸带上颜色的种类数。
第二行有 n 用空格隔开的正整数,第 i 个数字 numberi 表示纸带上编号为 i 格子上面写的数字。
第三行有 n 用空格隔开的正整数,第 i 数字 colori 表纸带上编号为 i 格子染的颜色。
输出格式
一个整数,表示所求的纸带分数除以 10007 所得的余数。
6 2
5 5 3 2 2 2
2 2 1 1 2 1
82
样例 1 说明
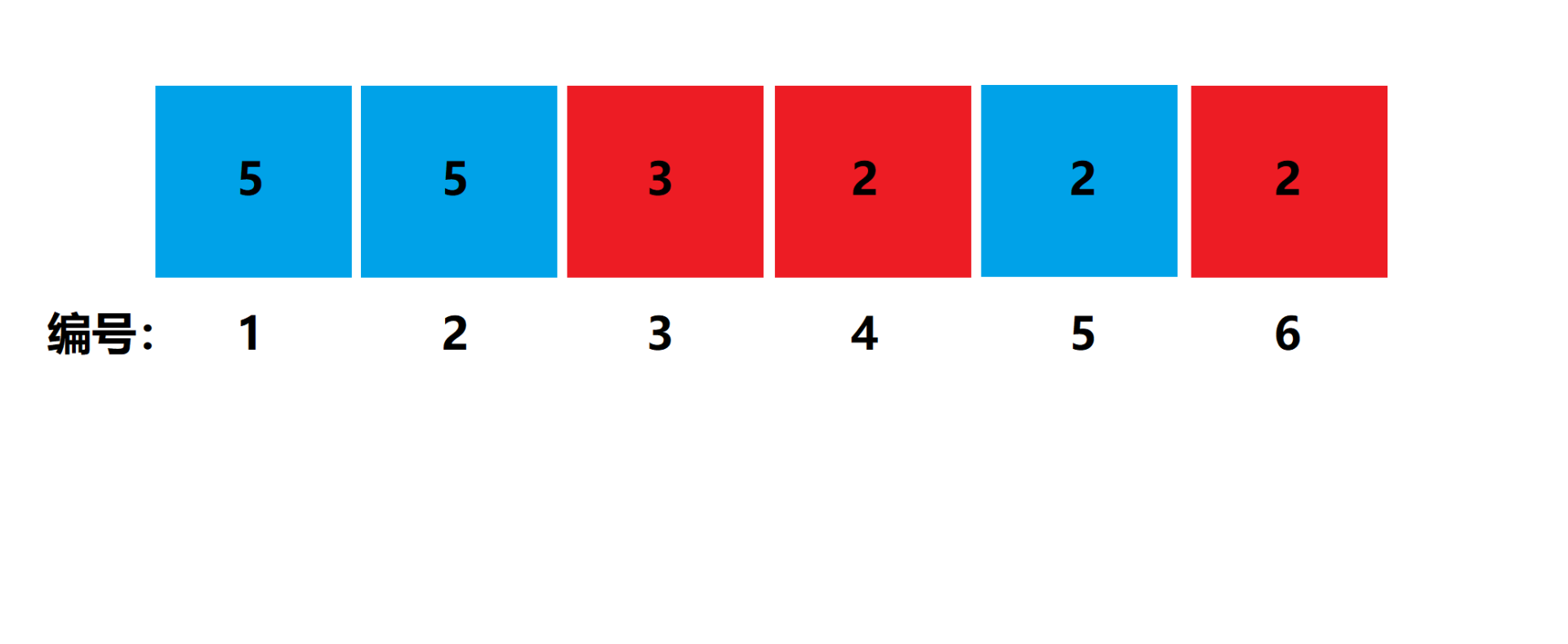
纸带如题目描述中的图所示。
所有满足条件的三元组为: (1,3,5) , (4,5,6) 。
所以纸带的分数为 (1+5) × (5+2) + (4+6) × (2+2) = 42 + 40 = 82 。
数据规模与约定
对于第 1 组至第 2 组数据, 1 ≤ n ≤ 100 , 1 ≤ m ≤ 5 ;
对于第 3 组至第 4 组数据, 1 ≤ n ≤ 3000 , 1 ≤ m ≤ 100 ;
对于第 5 组至第 6 组数据, 1 ≤ n ≤ 100000 , 1 ≤ m ≤ 100000 ,且不存在出现次数超过 20 的颜色;
对于全部 10 组数据 , 1 ≤ n ≤ 100000 , 1 ≤ m ≤ 100000 , 1 ≤ colori ≤ m , 1 ≤ numberi ≤ 100000 。

