Kavi on Pairing Duty

题面翻译

给定一条有 $2n$ 个点的直线，将上面的点两两配对形成圆弧，要求任意不等大的圆弧必然为包含关系。问合法的状态总数模 $998244353$。

如图，$A$ 与 $B$ 都是合法的；$C$ 不合法，因为红色圆弧与蓝色圆弧不等大且不交。

$n\leq 10^6$。

题目描述

Kavi has $2n$ points lying on the $OX$ axis, $i$ -th of which is located at $x = i$ .

Kavi considers all ways to split these $2n$ points into $n$ pairs. Among those, he is interested in good pairings, which are defined as follows:

Consider $n$ segments with ends at the points in correspondent pairs. The pairing is called good, if for every $2$ different segments $A$ and $B$ among those, at least one of the following holds:

• One of the segments $A$ and $B$ lies completely inside the other.
• $A$ and $B$ have the same length.

Consider the following example:

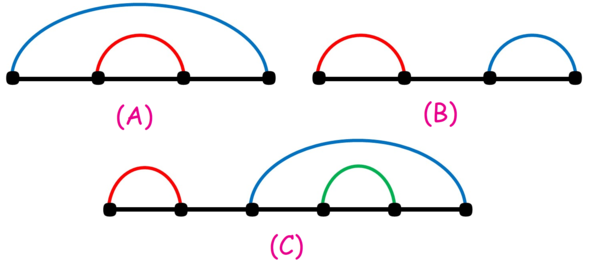$A$ is a good pairing since the red segment lies completely inside the blue segment.

$B$ is a good pairing since the red and the blue segment have the same length.

$C$ is not a good pairing since none of the red or blue segments lies inside the other, neither do they have the same size.

Kavi is interested in the number of good pairings, so he wants you to find it for him. As the result can be large, find this number modulo $998244353$ .

Two pairings are called different, if some two points are in one pair in some pairing and in different pairs in another.

输入格式

The single line of the input contains a single integer $n$ $(1\le n \le 10^6)$ .

输出格式

Print the number of good pairings modulo $998244353$ .

样例 #1

样例输入 #1

1

样例输出 #1

1

样例 #2

样例输入 #2

2

样例输出 #2

3

样例 #3

样例输入 #3

3

样例输出 #3

6

样例 #4

样例输入 #4

100

样例输出 #4

688750769

提示

The good pairings for the second example are:

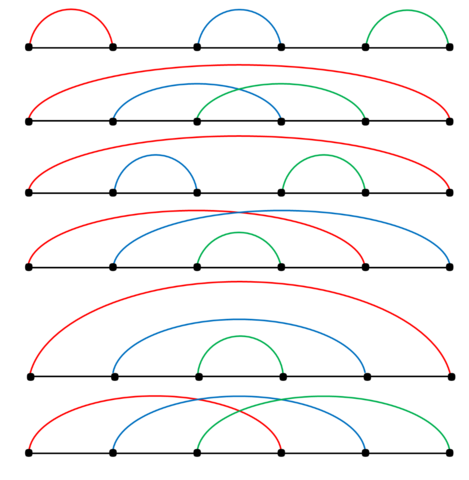
In the third example, the good pairings are: