#P6037. Ryoku 的探索
Ryoku 的探索
题目背景
Ryoku 对自己所处的世界充满了好奇,她希望能够在她「死」之前尽可能能多地探索世界。
这一天,Ryoku 得到了一张这个世界的地图,她十分高兴。然而,Ryoku 并不知道自己所处的位置到底在哪里,她也不知道她会什么时候死去。她想要知道如何才能尽可能多的探索这个世界。
题目描述
Ryoku 所处的世界可以抽象成一个有 个点, 条边的带权无向连通图 。每条边有美观度和长度。
Ryoku 会使用这样一个策略探索世界:在每个点寻找一个端点她未走过的边中美观度最高的走,如果没有边走,就沿着她前往这个点的边返回,类似于图的深度优先遍历。
探索的一个方案的长度是这个方案所经过的所有边长度的和(返回时经过的长度不用计算)。
她想知道,对于每一个起点 ,她需要走过的长度是多少?
输入格式
输入包含 行,其中第一行包含一个整数 。
接下来 行每行包含四个整数 ,描述了一条连接 和 ,长度为 ,美观度为 的无向边。
输出格式
输出包含 行,每行一个整数,第 行为 时的答案。
5
4 1 2 1
1 2 3 2
3 1 1 4
3 5 2 5
2 3 2 3
7
7
8
7
8
提示
【样例 1 说明】
以下为输入输出样例 1 中的图: (边上红色数组为 ,黑色为 )
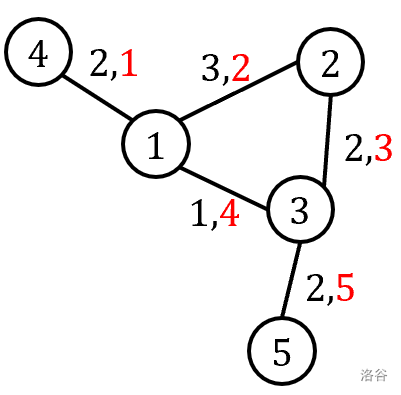
若起点为 ,顺序为 ,长度之和为 。
若起点为 ,顺序为 ,长度之和为 。
若起点为 ,顺序为 ,长度之和为 。
若起点为 ,顺序为 ,长度之和为 。
若起点为 ,顺序为 ,长度之和为 。
【数据规模与约定】
对于 的数据,。
对于 的数据,,,,保证 互不相同。
