题目背景

由于昨晚某个OIer卡IOIAKer大佬代码把std卡没了，所以IOIAKer把那个OIer拿来爆炒了，还叫上了大家一起来开美食盛宴。

这下面所有公式都是我乱写的，但一定能求出结果

题目描述

提前声明（桌子是一张）

作为一个签到小菜，这爆烤oier的火候得是：

$$x=\frac{\sin A+\sin B+\sin C}{\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2}}*\sum_{i=0}^{\infty} \frac{e^{i\pi}e^{i\pi}}{4i+1}-\frac{\sin A+\sin B+\sin C}{\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2}}*\sum_{i=1}^{\infty} {\frac{e^{i\pi}e^{i\pi}}{4i-1}} $$

这样的，没错，这是个无理数。

其中A,B,C是餐桌的3个角，据说要考虑到餐桌的形状才能做出美味的佳肴，餐桌如下：

而又众所周知，煎OIer需要一个平底锅：

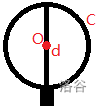
但是由于IOIAKer觉得这个公式算出来的火候有点小，于是（：

$$(2x+\sum_{i=1}^n a_i*x)3x^2$$

当然，火候也要考虑到平底锅的一些参数：

$$\frac{(2x+\sum_{i=1}^n a_i*x)3x^2}{(\frac{C}{d})^3} $$

好了，使用上面的这个火候你就能炒出一个完美的OIer，但是IOIAKer要考考你，才能让你吃到OIer，请说出最终的火候的数值吧（结果保留整数）。

输入格式

第一行，一个数，表示$d$（你应该能自己求出$C$）

第二行，有一个数$n$。

第三行，有$n$个数，第$i$个数表示$a_i$

输出格式

一个整数，表示火候

样例

9109823
10
1 2 3 4 5 6 7 8 9 10

171

提示/说明

$1\le n,a_i \le 4*10^4,1\leq d \leq 10^9$

出题人还特别良心的把样例放到数据里给大家骗分，但其他的数据出题人可不会手下留情

众所周知，IOIAKer有个巨大的平底锅